diff --git a/SLIDES/lecture-01-introduction-installation.md b/SLIDES/lecture-01-introduction-installation.md
deleted file mode 100644
index ea515bb..0000000
--- a/SLIDES/lecture-01-introduction-installation.md
+++ /dev/null
@@ -1,817 +0,0 @@
----
-marp: true
-title: R for modellers - Lecture 01 - Introduction to R. Installing R
-description: Julien Arino - Lecture 01 - R for modellers - Introduction to R. Installing R.
-theme: default
-paginate: false
-math: mathjax
-size: 16:9
----
-
-
-
-
-# Lecture 01 - Introduction to R. Installing R
-
-Julien Arino [](mailto:Julien.Arino@umanitoba.ca) [](https://julien-arino.github.io/) [](https://github.com/julien-arino)
-
-Department of Mathematics & Data Science Nexus
-University of Manitoba*
-
-
-
-Canadian Centre for Disease Modelling
-
-
-* The University of Manitoba campuses are located on original lands of Anishinaabeg, Cree, Oji-Cree, Dakota and Dene peoples, and on the homeland of the Métis Nation.
-
----
-
-
-# Outline
-
-- Foreword: the R language
-- Programming in R
-- Dealing with data
-- Solving ODE numerically
-
----
-
-
-# Foreword: the R language
-
----
-
-# R was originally for stats but is now more
-
-- Open source version of S
-- Appeared in 1993
-- Now version 4.2
-- One major advantage in my view: uses a lot of C and Fortran code. E.g., `deSolve`:
-> The functions provide an interface to the FORTRAN functions 'lsoda', 'lsodar', 'lsode', 'lsodes' of the 'ODEPACK' collection, to the FORTRAN functions 'dvode', 'zvode' and 'daspk' and a C-implementation of solvers of the 'Runge-Kutta' family with fixed or variable time steps
-- Very active community on the web, easy to find solutions (same true of Python, I just prefer R)
-
----
-
-# Development environments
-
-- Terminal version, not very friendly
-- Nicer terminal: [radian](https://github.com/randy3k/radian)
-- Execute R scripts by using `Rscript name_of_script.R`. Useful to run code in `cron`, for instance
-- Use IDEs:
- - [RStudio](https://www.rstudio.com/products/rstudio/) has become the reference
- - [RKWard](https://invent.kde.org/education/rkward) is useful if you are for instance using an ARM processor (Raspberry Pi, some Chromebooks..)
-- Integrate into jupyter notebooks
-
----
-
-# Going further
-
-- [RStudio server](https://www.rstudio.com/products/rstudio/#rstudio-server): run RStudio on a Linux server and connect via a web interface
-- Shiny: easily create an interactive web site running R code
-- [Shiny server](https://www.rstudio.com/products/shiny/shiny-server/): run Shiny apps on a Linux server
-- Rmarkdown: markdown that incorporates R commands. Useful for generating reports in html or pdf, can make slides as well..
-- RSweave: LaTeX incorporating R commands. Useful for generating reports. Not used as much as Rmarkdown these days
-
----
-
-# R is a scripted language
-
-- Interactive
-- Allows you to work in real time
- - Be careful: what is in memory might involve steps not written down in a script
- - If you want to reproduce your steps, it is good to write all the steps down in a script and to test from time to time running using `Rscript`: this will ensure that all that is required to run is indeed loaded to memory when it needs to, i.e., that it is not already there..
-
----
-
-
-# Programming in R
-
----
-
-# Similar to matlab..
-
-.. with some differences, of course! Otherwise, where would the fun be? ;)
-
----
-
-# Assignment
-
-Two ways:
-
-```
-X <- 10
-```
-
-or
-
-```
-X = 10
-```
-
-First version is preferred by R purists.. I don't really care
-
----
-
-# Lists
-
-A very useful data structure, quite flexible and versatile. Empty list: `L <- list()`. Convenient for things like parameters. For instance
-
-```
-L <- list()
-L$a <- 10
-L$b <- 3
-L[["another_name"]] <- "Plouf plouf"
-```
-
-```
-> L[1]
-$a
-[1] 10
-> L[[2]]
-[1] 3
-> L$a
-[1] 10
-> L[["b"]]
-[1] 3
-> L$another_name
-[1] "Plouf plouf"
-```
-
----
-
-# Vectors
-
-```
-x = 1:10
-y <- c(x, 12)
-> y
- [1] 1 2 3 4 5 6 7 8 9 10 12
-z = c("red", "blue")
-> z
-[1] "red" "blue"
-z = c(z, 1)
-> z
-[1] "red" "blue" "1"
-```
-Note that in `z`, since the first two entries are characters, the added entry is also a character. Contrary to lists, vectors have all entries of the same type
-
----
-
-# Matrices
-
-Matrix (or vector) of zeros
-```
-A <- mat.or.vec(nr = 2, nc = 3)
-```
-
-Matrix with prescribed entries
-
-```
-B <- matrix(c(1,2,3,4), nr = 2, nc = 2)
-> B
- [,1] [,2]
-[1,] 1 3
-[2,] 2 4
-C <- matrix(c(1,2,3,4), nr = 2, nc = 2, byrow = TRUE)
-> C
- [,1] [,2]
-[1,] 1 2
-[2,] 3 4
-```
-
-Remark that here and elsewhere, naming the arguments (e.g., `nr = 2`) allows to use arguments in any order
-
----
-
-# Matrix operations
-
-Probably the biggest annoyance in R compared to other languages
-
-- The notation `A*B` is the *Hadamard product* $A\circ B$ (what would be denoted `A.*B` in matlab), not the standard matrix multiplication
-- Matrix multiplication is written `A %*% B`
-
----
-
-# Vector operations
-
-Vector addition is also frustrating. Say you write `x=1:10`, i.e., make the vector
-```
-> x
- [1] 1 2 3 4 5 6 7 8 9 10
-```
-Then `x+1` gives
-```
-> x+1
- [1] 2 3 4 5 6 7 8 9 10 11
- ```
- i.e., adds 1 to all entries in the vector
-
- Beware of this in particular when addressing sets of indices in lists, vectors or matrices
-
----
-
-# For the matlab-ers here
-
-- R does not have the keyword `end` to access the last entry in a matrix/vector/list..
-- Use `length` (lists or vectors), `nchar` (character chains), `dim` (matrices.. careful, of course returns 2 values)
-
----
-
-# Flow control
-
-```
-if (condition is true) {
- list of stuff to do
-}
-```
-
-Even if `list of stuff to do` is a single instruction, best to use curly braces
-
-```
-if (condition is true) {
- list of stuff to do
-} else if (another condition) {
- ...
-} else {
- ...
-}
-```
-
----
-
-# For loops
-
-`for` applies to lists or vectors
-
-```
-for (i in 1:10) {
- something using integer i
-}
-for (j in c(1,3,4)) {
- something using integer j
-}
-for (n in c("truc", "muche", "chose")) {
- something using string n
-}
-for (m in list("truc", "muche", "chose", 1, 2)) {
- something using string n or integer n, depending
-}
-```
-
----
-
-# lapply
-
-Very useful function (a few others in the same spirit: `sapply`, `vapply`, `mapply`)
-
-Applies a function to each entry in a list/vector/matrix
-
-Because there is a parallel version (`parLapply`) that we will see later, worth learning
-
-```
-l = list()
-for (i in 1:10) {
- l[[i]] = runif(i)
-}
-lapply(X = l, FUN = mean)
-```
-
-or, to make a vector
-
-```
-unlist(lapply(X = l, FUN = mean))
-```
-
-or
-
-```
-sapply(X = l, FUN = mean)
-```
-
----
-
-# "Advanced" lapply
-
-Can "pick up" nontrivial list entries
-
-```
-l = list()
-for (i in 1:10) {
- l[[i]] = list()
- l[[i]]$a = runif(i)
- l[[i]]$b = runif(2*i)
-}
-sapply(X = l, FUN = function(x) length(x$b))
-```
-
-gives
-
-```
-[1] 2 4 6 8 10 12 14 16 18 20
-```
-
-Just recall: the argument to the function you define is a list entry (`l[[1]]`, `l[[2]]`, etc., here)
-
----
-
-# Avoid parameter variation loops with expand.grid
-
-```
-# Suppose we want to vary 3 parameters
-variations = list(
- p1 = seq(1, 10, length.out = 10),
- p2 = seq(0, 1, length.out = 10),
- p3 = seq(-1, 1, length.out = 10)
-)
-
-# Create the list
-tmp = expand.grid(variations)
-PARAMS = list()
-for (i in 1:dim(tmp)[1]) {
- PARAMS[[i]] = list()
- for (k in 1:length(variations)) {
- PARAMS[[i]][[names(variations)[k]]] = tmp[i, k]
- }
-}
-```
-
-There is still a loop, but you can split this list, use it on different machines, etc. And can use `parLapply`
-
----
-
-
-# Dealing with data
-
-- Example: population of South Africa
-- Example - Dutch Elm Disease
-- Data wrangling
-
-
-
-
-- JA. [Mathematical epidemiology in a data-rich world](http://dx.doi.org/10.1016/j.idm.2019.12.008). *Infectious Disease Modelling* **5**:161-188 (2020)
-- See also [GitHub repo](https://github.com/julien-arino/modelling-with-data) for that paper
-
-
-
----
-
-# It is important to be "data aware"
-
-- Using R (or Python), it is really easy to grab data from the web, e.g., from Open Data sources
-- More and more locations have an open data policy
-- As a modeller, you do not need to have data everywhere, but you should be aware of the context
-- If you want your work to have an impact, for instance in public health, you cannot be completely disconnected from reality
-
----
-
-# Data is everywhere
-
-## Closed data
-
-- Often generated by companies, governments or research labs
-- When available, come with multiple restrictions
-
-## Open data
-
-- Often generated by the same entities but "liberated" after a certain period
-- More and more frequent with governments/public entities
-- Wide variety of licenses, so beware
-- Wide variety of qualities, so beware
-
----
-
-# Open Data initiatives
-
-Recent movement (5-10 years): governments (local or higher) create portals where data are centralised and published
-
-- [Winnipeg](https://data.winnipeg.ca/)
-- [Alberta](https://open.alberta.ca/opendata)
-- [Canada](https://open.canada.ca/en/open-data)
-- [Europe](https://data.europa.eu/euodp/data/)
-- [UN](http://data.un.org/)
-- [World Bank](https://data.worldbank.org/)
-- [WHO](https://www.who.int/gho/database/en/)
-
----
-
-# Data gathering methods
-
-- By hand
-- Using programs such as [Engauge Digitizer](http://markummitchell.github.io/engauge-digitizer/) or [g3data](https://github.com/pn2200/g3data)
-- Using APIs
-- Using natural language processing and other web scraping methods
-- Using R or Python packages
-
----
-
-
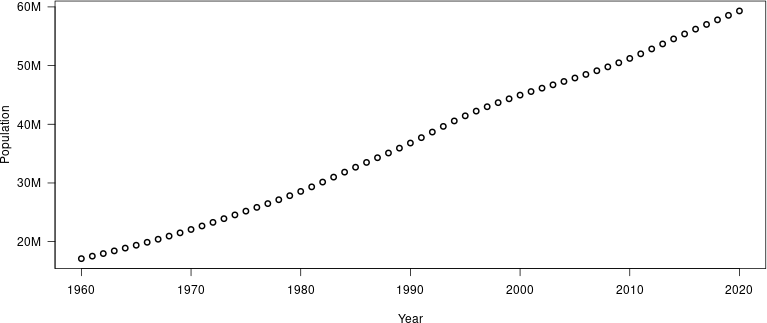
-# Example: population of South Africa
-
----
-
-```
-library(wbstats)
-pop_data_CTRY <- wb_data(country = "ZAF", indicator = "SP.POP.TOTL",
- mrv = 100, return_wide = FALSE)
-y_range = range(pop_data_CTRY$value)
-y_axis <- make_y_axis(y_range)
-png(file = "pop_ZAF.png",
- width = 800, height = 400)
-plot(pop_data_CTRY$date, pop_data_CTRY$value * y_axis$factor,
- xlab = "Year", ylab = "Population", type = "b", lwd = 2,
- yaxt = "n")
-axis(2, at = y_axis$ticks, labels = y_axis$labels, las = 1)
-dev.off()
-crop_figure("pop_ZAF.png")
-```
-
----
-
-
-
----
-
-
-# Example - Dutch Elm Disease
-
----
-# Dutch Elm Disease
-
-- Fungal disease that affects Elms
-- Caused by the fungus *Ophiostoma ulmi*
-- Transmitted by the Elm bark beetle (*Scolytus scolytus*)
-- Has decimated North American urban elm forests
-
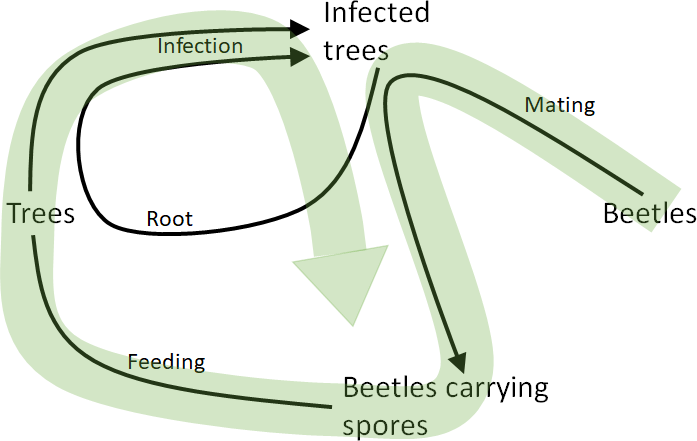
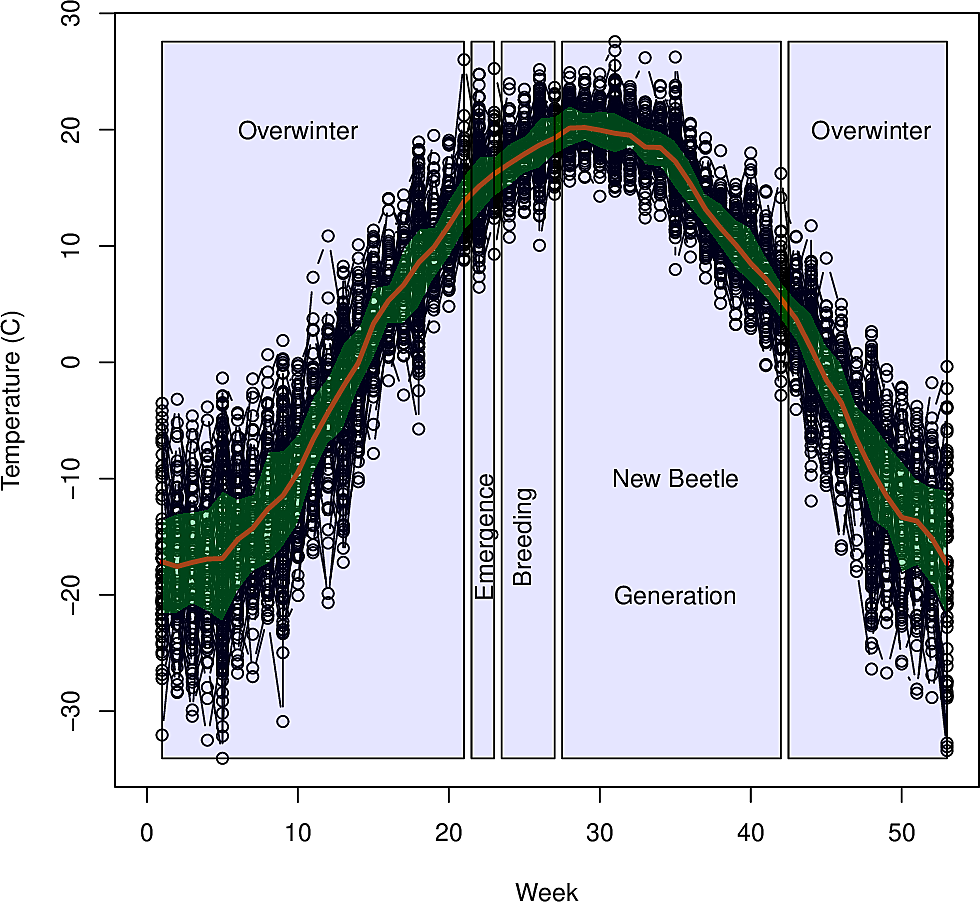
----
-
-
-
----
-
-
-
----
-
-
-
----
-
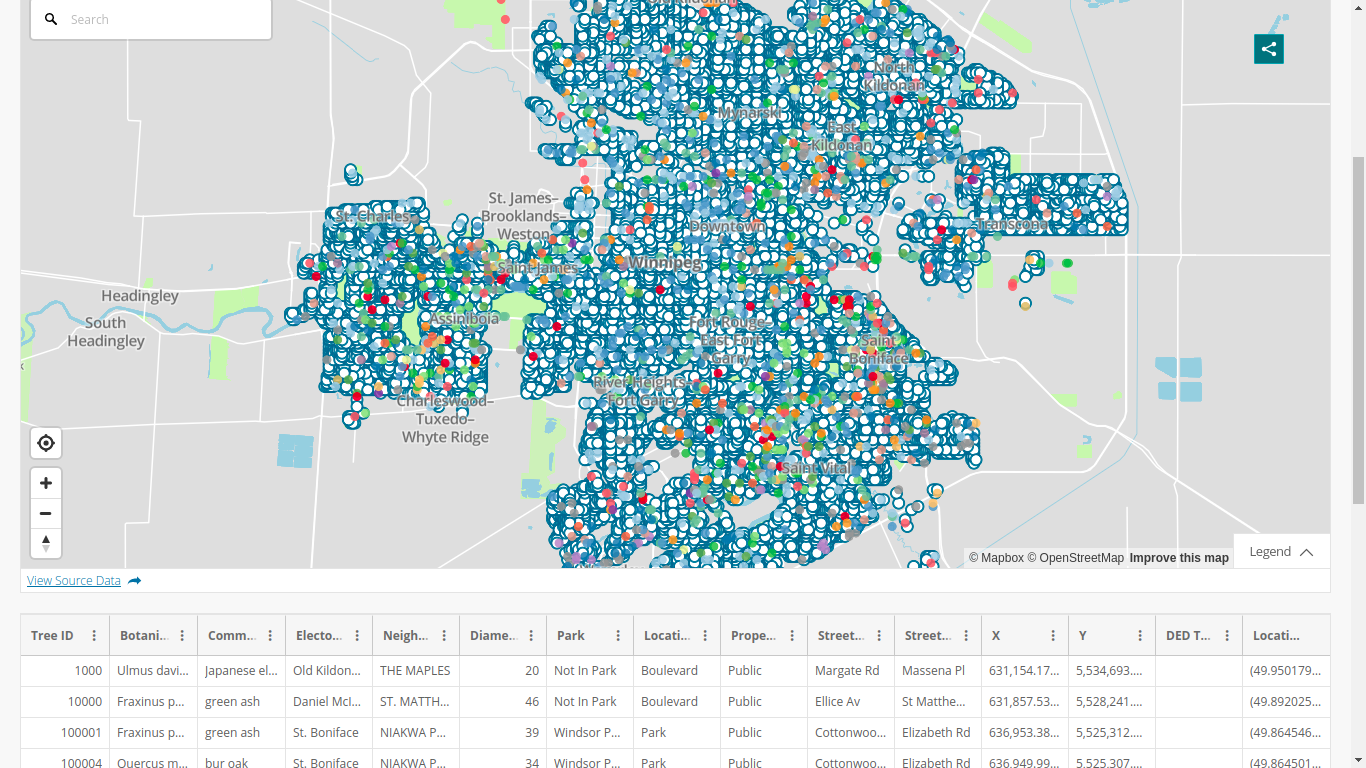
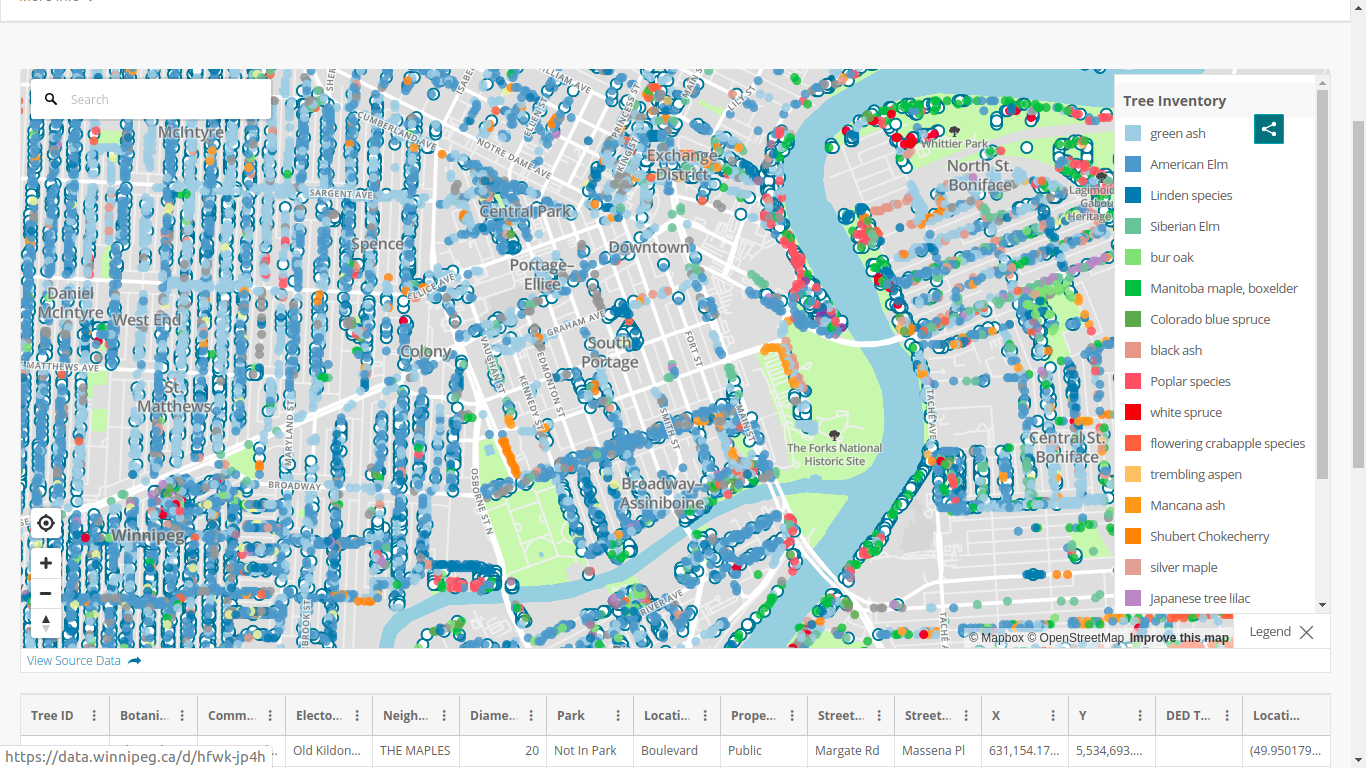
-# Getting the tree data
-
-```
-allTrees = read.csv("https://data.winnipeg.ca/api/views/hfwk-jp4h/ro
-```
-
-After this,
-
-```
-dim(allTrees)
-## [1] 300846
-15
-```
-
----
-
-# Let us clean things a little
-
-```
-elms_idx = grep("American Elm", allTrees$Common.Name, ignore.case = TRUE)
-elms = allTrees[elms_idx, ]
-```
-
-We are left with 54,036 American elms
-
----
-
-
-
----
-
-
-
----
-
-# Computation of root systems interactions
-
-(Needs a relatively large machine here - about 50GB RAM)
-
-- If roots of an infected tree touch roots of a susceptible tree, fungus is transmitted
-- Spread of a tree's root system depends on its height (we have diametre at breast height, DBH, for all trees)
-- The way roadways are built, there cannot be contacts between root systems of trees on opposite sides of a street
-
----
-
-# Distances between all trees
-
-```
-elms_xy = cbind(elms$X, elms$Y)
-D = dist(elms_xy)
-idx_D = which(D<50)
-```
-
-`indices_LT` is a large $N(N-1)/2\times 2$ matrix with indices (orig,dest) of trees in the pairs of elms, so `indices_LT[idx_D]` are the pairs under consideration
-
-Keep a little more..
-
-```
-indices_LT_kept = as.data.frame(cbind(indices_LT[idx_D,],
- D[idx_D]))
-colnames(indices_LT_kept) = c("i","j","dist")
-```
-
----
-
-# Create line segments between all pairs of trees
-
-```
-tree_locs_orig = cbind(elms_latlon$lon[indices_LT_kept$i],
- elms_latlon$lat[indices_LT_kept$i])
-tree_locs_dest = cbind(elms_latlon$lon[indices_LT_kept$j],
- elms_latlon$lat[indices_LT_kept$j])
-tree_pairs = do.call(
- sf::st_sfc,
- lapply(
- 1:nrow(tree_locs_orig),
- function(i){
- sf::st_linestring(
- matrix(
- c(tree_locs_orig[i,],
- tree_locs_dest[i,]),
- ncol=2,
- byrow=TRUE)
- )
- }
- )
-)
-```
-
----
-
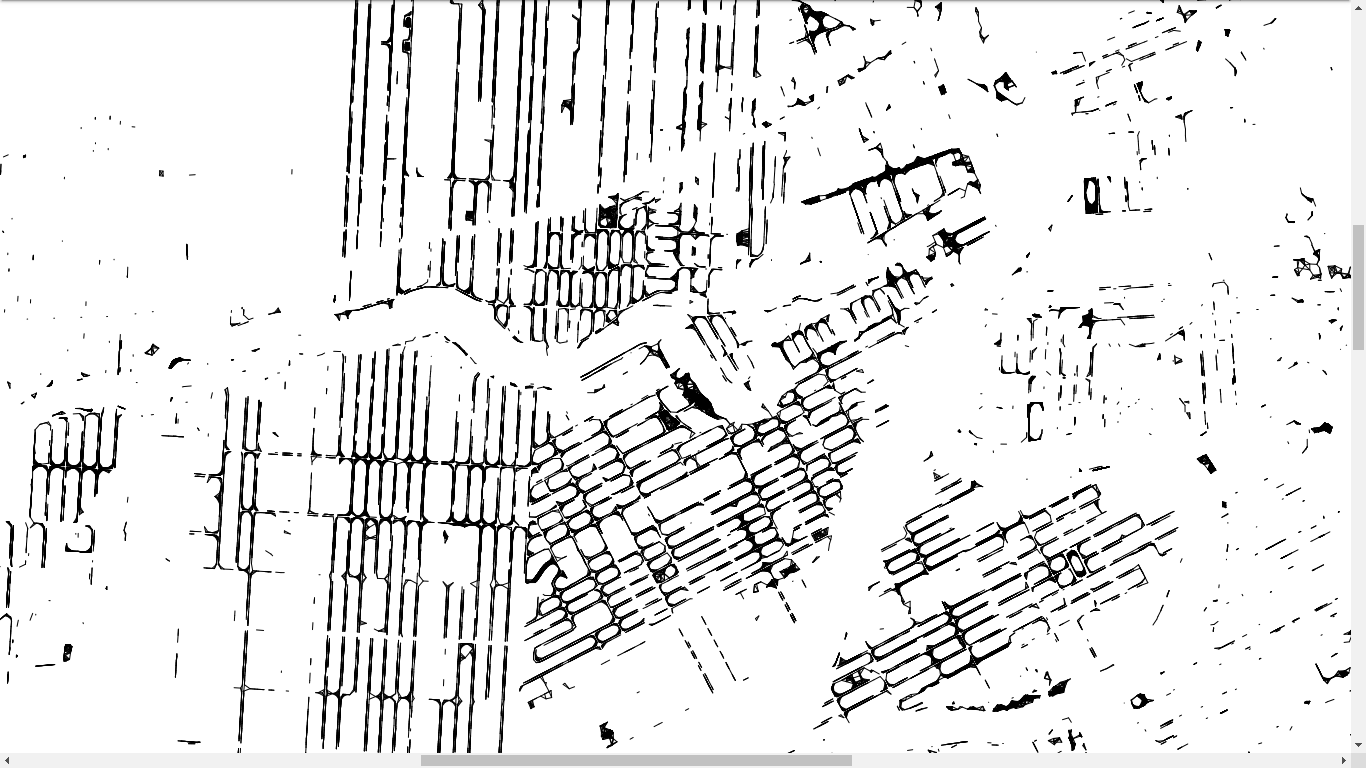
-# A bit of mapping
-
-```
-library(tidyverse)
-# Get bounding polygon for Winnipeg
-bb_poly = osmdata::getbb(place_name = "winnipeg",
- format_out = "polygon")
-# Get roads
-roads <- osmdata::opq(bbox = bb_poly) %>%
- osmdata::add_osm_feature(key = 'highway',
- value = 'residential') %>%
- osmdata::osmdata_sf () %>%
- osmdata::trim_osmdata (bb_poly)
-# Get rivers
-rivers <- osmdata::opq(bbox = bb_poly) %>%
- osmdata::add_osm_feature(key = 'waterway',
- value = "river") %>%
- osmdata::osmdata_sf () %>%
- osmdata::trim_osmdata (bb_poly)
-```
-
----
-
-# And we finish easily
-
-- We have the pairs of trees potentially in contact with each other
-- We have the roads and rivers of the city, which is a collection of line segments
-- If there is an intersection between a tree pair and a road/river, then we can forget this tree pair as their root systems cannot come into contact
-
-```
-st_crs(tree_pairs) = sf::st_crs(roads$osm_lines$geometry)
-iroads = sf::st_intersects(x = roads$osm_lines$geometry,
- y = tree_pairs)
-irivers = sf::st_intersects(x = rivers$osm_lines$geometry,
- y = tree_pairs)
-```
-
----
-
-```
-tree_pairs_roads_intersect = c()
-for (i in 1:length(iroads)) {
- if (length(iroads[[i]])>0) {
- tree_pairs_roads_intersect = c(tree_pairs_roads_intersect,
- iroads[[i]])
- }
-}
-tree_pairs_roads_intersect = sort(tree_pairs_roads_intersect)
-to_keep = 1:dim(tree_locs_orig)[1]
-to_keep = setdiff(to_keep,tree_pairs_roads_intersect)
-```
-
----
-
-
-
----
-
-
-# Data wrangling
-
----
-
-# Data wrangling: `dplyr` vs `sqldf`
-
-`dplyr` is part of the `tidyverse` set of libraries. Load `magrittr` and its pipe `%>%`
-
-`sqldf` allows to use SQL on dataframes.. interesting alternative if you know SQL
-
----
-
-```
-library(sqldf)
-library(dplyr)
-
-SARS = read.csv("../DATA/SARS-CoV-1_data.csv")
-
-## Three ways to keep only the data for one country
-ctry = "Canada"
-# The basic one
-idx = which(SARS$country == ctry)
-SARS_selected = SARS[idx,]
-# The sqldf way
-SARS_selected = sqldf(paste0("SELECT * FROM SARS WHERE country = '",
- ctry, "'"))
-# The dplyr way
-SARS_selected = SARS %>%
- filter(country == ctry)
-```
-
----
-
-```
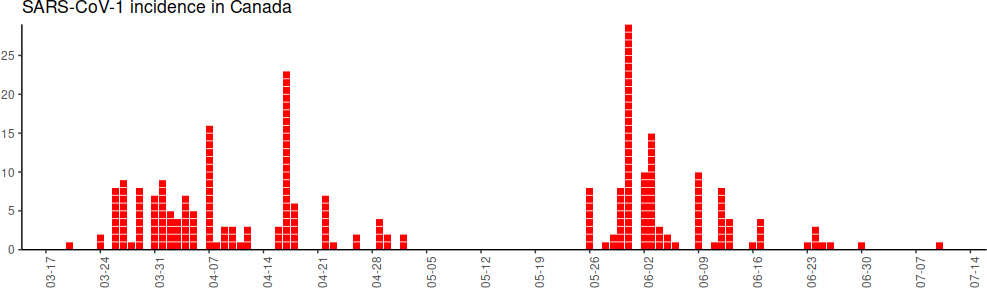
-# Create incidence for the selected country. diff does difference one by one,
-# so one less entry than the vector on which it is being used, thus we pad with a 0.
-SARS_selected$incidence = c(0, diff(SARS_selected$totalNumberCases))
-# Keep only positive incidences (discard 0 or negative adjustments)
-SARS_selected = SARS_selected %>%
- filter(incidence > 0)
-
-# Plot the result
-# Before plotting, we need to make the dates column we will use be actual dates..
-SARS_selected$toDate = lubridate::ymd(SARS_selected$toDate)
-EpiCurve(SARS_selected,
- date = "toDate", period = "day",
- freq = "incidence",
- title = "SARS-CoV-1 incidence in Canada in 2003")
-```
-
----
-
-
-
----
-
-
-# Solving ODE numerically
-
-- The deSolve library
-- Example - Fitting data
-
----
-
-
-# The deSolve library
-
----
-
-# The deSolve library
-
-- As I have already pointed out, [`deSolve`](https://cran.r-project.org/web/packages/deSolve/index.html):
-> The functions provide an interface to the FORTRAN functions 'lsoda', 'lsodar', 'lsode', 'lsodes' of the 'ODEPACK' collection, to the FORTRAN functions 'dvode', 'zvode' and 'daspk' and a C-implementation of solvers of the 'Runge-Kutta' family with fixed or variable time steps
-
-- So you are benefiting from years and year of experience: [ODEPACK](https://computing.llnl.gov/projects/odepack) is a set of Fortran (77!) solvers developed at Lawrence Livermore National Laboratory (LLNL) starting in the late 70s
-
-- Other good solvers are also included, those written in C
-
-- Refer to the [package help](https://cran.r-project.org/web/packages/deSolve/deSolve.pdf) for details
-
----
-
-# Using deSolve for simple ODEs
-
-As with more numerical solvers, you need to write a function returning the value of the right hand side of your equation (the vector field) at a given point in phase space, then call this function from the solver
-
-```
-library(deSolve)
-rhs_logistic <- function(t, x, p) {
- with(as.list(x), {
- dN <- p$r * N *(1-N/p$K)
- return(list(dN))
- })
-}
-params = list(r = 0.1, K = 100)
-IC = c(N = 50)
-times = seq(0, 100, 1)
-sol <- ode(IC, times, rhs_logistic, params)
-```
-
----
-
-This also works: add `p` to arguments of `as.list` and thus use without `p$` prefix
-
-```
-library(deSolve)
-rhs_logistic <- function(t, x, p) {
- with(as.list(c(x, p)), {
- dN <- r * N *(1-N/K)
- return(list(dN))
- })
-}
-params = list(r = 0.1, K = 100)
-IC = c(N = 50)
-times = seq(0, 100, 1)
-sol <- ode(IC, times, rhs_logistic, params)
-```
-
-In this case, beware of not having a variable and a parameter with the same name..
-
----
-
-# Default method: `lsoda`
-
-- `lsoda` switches automatically between stiff and nonstiff methods
-
-- You can also specify other methods: "lsode", "lsodes", "lsodar", "vode", "daspk", "euler", "rk4", "ode23", "ode45", "radau", "bdf", "bdf_d", "adams", "impAdams" or "impAdams_d" ,"iteration" (the latter for discrete-time systems)
-
-```
-ode(y, times, func, parms,
- method = "ode45")
-```
-
-- You can even implement your own integration method
-
----
-
-
-# Example - Fitting data
-
----
-
-# Example - Fitting data
-
-- Note that this is a super simplified version of what to do
-- Much more elaborate procedures exist
- - Roda. [Bayesian inference for dynamical systems](https://doi.org/10.1016/j.idm.2019.12.007)
- - Portet. [A primer on model selection using the Akaike Information Criterion](https://doi.org/10.1016/j.idm.2019.12.010)
-- Let us grab some epi data online and fit an SIR model to it
-- Don't expect anything funky, as I said, this is the baby version
-- Also, keep in mind that any identification procedure is subject to risks due to *identifiability issues*; see, e.g., Roda et al, [Why is it difficult to accurately predict the COVID-19 epidemic?](https://doi.org/10.1016/j.idm.2020.03.001)
-
----
-
-# Principle
-
-- Data is a set $(t_i,y_i)$, $i=1,\ldots,N$, where $t_i\in\mathcal{I}$, some interval
-- Solution to SIR is $(t,x(t))$ for $t\in\mathcal{I}$
-- Suppose parameters of the model are $p$
-- We want to minimise the error function
-$$
-E(p) = \sum_{i=1}^N \|x(t_i)-y_i\|
-$$
-- Norm is typically Euclidean, but could be different depending on objectives
-- So given a point $p$ in (admissible) parameter space, we compute the solution to the ODE, compute $E(p)$
-- Using some minimisation algorithm, we seek a minimum of $E(p)$ by varying $p$
-
----
-
-# What are $y_i$ and $x(t_i)$ here?
-
-- In epi data for infectious diseases, we typically have incidence, i.e., number of new cases per unit time
-- In SIR model, this is $\beta SI$ or $\beta SI/N$, so, if using mass action incidence and Euclidean norm
-$$
-E(p)=\sum_{i=1}^N(\beta S(t_i)I(t_i)-y_i)^2
-$$
-or, if using standard incidence
-$$
-E(p)=\sum_{i=1}^N
-\left(\beta \frac{S(t_i)I(t_i)}{N}-y_i\right)^2
-$$
-
----
-
-# Implementing in practice
-
-See the code [practicum_01_fitting.R](https://raw.githubusercontent.com/julien-arino/3MC-course-epidemiological-modelling/main/CODE/practicum_01_fitting.R), which we will go over now
\ No newline at end of file
diff --git a/SLIDES/lecture-06-solving-ODE.md b/SLIDES/lecture-06-solving-ODE.md
deleted file mode 100644
index 2597fd5..0000000
--- a/SLIDES/lecture-06-solving-ODE.md
+++ /dev/null
@@ -1,817 +0,0 @@
----
-marp: true
-title: R for modellers - Lecture 01 - Introduction to R. Installing R
-description: Julien Arino - Lecture 01 - R for modellers - Introduction to R. Installing R.
-theme: default
-paginate: false
-math: mathjax
-size: 16:9
----
-
-
-
-
-# Lecture 01 - Introduction to R. Installing R
-
-Julien Arino [](mailto:Julien.Arino@umanitoba.ca) [](https://julien-arino.github.io/) [](https://github.com/julien-arino)
-
-Department of Mathematics
-University of Manitoba*
-
-
-
-Canadian Centre for Disease Modelling
-
-
-* The University of Manitoba campuses are located on original lands of Anishinaabeg, Cree, Oji-Cree, Dakota and Dene peoples, and on the homeland of the Métis Nation.
-
----
-
-
-# Outline
-
-- Foreword: the R language
-- Programming in R
-- Dealing with data
-- Solving ODE numerically
-
----
-
-
-# Foreword: the R language
-
----
-
-# R was originally for stats but is now more
-
-- Open source version of S
-- Appeared in 1993
-- Now version 4.2
-- One major advantage in my view: uses a lot of C and Fortran code. E.g., `deSolve`:
-> The functions provide an interface to the FORTRAN functions 'lsoda', 'lsodar', 'lsode', 'lsodes' of the 'ODEPACK' collection, to the FORTRAN functions 'dvode', 'zvode' and 'daspk' and a C-implementation of solvers of the 'Runge-Kutta' family with fixed or variable time steps
-- Very active community on the web, easy to find solutions (same true of Python, I just prefer R)
-
----
-
-# Development environments
-
-- Terminal version, not very friendly
-- Nicer terminal: [radian](https://github.com/randy3k/radian)
-- Execute R scripts by using `Rscript name_of_script.R`. Useful to run code in `cron`, for instance
-- Use IDEs:
- - [RStudio](https://www.rstudio.com/products/rstudio/) has become the reference
- - [RKWard](https://invent.kde.org/education/rkward) is useful if you are for instance using an ARM processor (Raspberry Pi, some Chromebooks..)
-- Integrate into jupyter notebooks
-
----
-
-# Going further
-
-- [RStudio server](https://www.rstudio.com/products/rstudio/#rstudio-server): run RStudio on a Linux server and connect via a web interface
-- Shiny: easily create an interactive web site running R code
-- [Shiny server](https://www.rstudio.com/products/shiny/shiny-server/): run Shiny apps on a Linux server
-- Rmarkdown: markdown that incorporates R commands. Useful for generating reports in html or pdf, can make slides as well..
-- RSweave: LaTeX incorporating R commands. Useful for generating reports. Not used as much as Rmarkdown these days
-
----
-
-# R is a scripted language
-
-- Interactive
-- Allows you to work in real time
- - Be careful: what is in memory might involve steps not written down in a script
- - If you want to reproduce your steps, it is good to write all the steps down in a script and to test from time to time running using `Rscript`: this will ensure that all that is required to run is indeed loaded to memory when it needs to, i.e., that it is not already there..
-
----
-
-
-# Programming in R
-
----
-
-# Similar to matlab..
-
-.. with some differences, of course! Otherwise, where would the fun be? ;)
-
----
-
-# Assignment
-
-Two ways:
-
-```
-X <- 10
-```
-
-or
-
-```
-X = 10
-```
-
-First version is preferred by R purists.. I don't really care
-
----
-
-# Lists
-
-A very useful data structure, quite flexible and versatile. Empty list: `L <- list()`. Convenient for things like parameters. For instance
-
-```
-L <- list()
-L$a <- 10
-L$b <- 3
-L[["another_name"]] <- "Plouf plouf"
-```
-
-```
-> L[1]
-$a
-[1] 10
-> L[[2]]
-[1] 3
-> L$a
-[1] 10
-> L[["b"]]
-[1] 3
-> L$another_name
-[1] "Plouf plouf"
-```
-
----
-
-# Vectors
-
-```
-x = 1:10
-y <- c(x, 12)
-> y
- [1] 1 2 3 4 5 6 7 8 9 10 12
-z = c("red", "blue")
-> z
-[1] "red" "blue"
-z = c(z, 1)
-> z
-[1] "red" "blue" "1"
-```
-Note that in `z`, since the first two entries are characters, the added entry is also a character. Contrary to lists, vectors have all entries of the same type
-
----
-
-# Matrices
-
-Matrix (or vector) of zeros
-```
-A <- mat.or.vec(nr = 2, nc = 3)
-```
-
-Matrix with prescribed entries
-
-```
-B <- matrix(c(1,2,3,4), nr = 2, nc = 2)
-> B
- [,1] [,2]
-[1,] 1 3
-[2,] 2 4
-C <- matrix(c(1,2,3,4), nr = 2, nc = 2, byrow = TRUE)
-> C
- [,1] [,2]
-[1,] 1 2
-[2,] 3 4
-```
-
-Remark that here and elsewhere, naming the arguments (e.g., `nr = 2`) allows to use arguments in any order
-
----
-
-# Matrix operations
-
-Probably the biggest annoyance in R compared to other languages
-
-- The notation `A*B` is the *Hadamard product* $A\circ B$ (what would be denoted `A.*B` in matlab), not the standard matrix multiplication
-- Matrix multiplication is written `A %*% B`
-
----
-
-# Vector operations
-
-Vector addition is also frustrating. Say you write `x=1:10`, i.e., make the vector
-```
-> x
- [1] 1 2 3 4 5 6 7 8 9 10
-```
-Then `x+1` gives
-```
-> x+1
- [1] 2 3 4 5 6 7 8 9 10 11
- ```
- i.e., adds 1 to all entries in the vector
-
- Beware of this in particular when addressing sets of indices in lists, vectors or matrices
-
----
-
-# For the matlab-ers here
-
-- R does not have the keyword `end` to access the last entry in a matrix/vector/list..
-- Use `length` (lists or vectors), `nchar` (character chains), `dim` (matrices.. careful, of course returns 2 values)
-
----
-
-# Flow control
-
-```
-if (condition is true) {
- list of stuff to do
-}
-```
-
-Even if `list of stuff to do` is a single instruction, best to use curly braces
-
-```
-if (condition is true) {
- list of stuff to do
-} else if (another condition) {
- ...
-} else {
- ...
-}
-```
-
----
-
-# For loops
-
-`for` applies to lists or vectors
-
-```
-for (i in 1:10) {
- something using integer i
-}
-for (j in c(1,3,4)) {
- something using integer j
-}
-for (n in c("truc", "muche", "chose")) {
- something using string n
-}
-for (m in list("truc", "muche", "chose", 1, 2)) {
- something using string n or integer n, depending
-}
-```
-
----
-
-# lapply
-
-Very useful function (a few others in the same spirit: `sapply`, `vapply`, `mapply`)
-
-Applies a function to each entry in a list/vector/matrix
-
-Because there is a parallel version (`parLapply`) that we will see later, worth learning
-
-```
-l = list()
-for (i in 1:10) {
- l[[i]] = runif(i)
-}
-lapply(X = l, FUN = mean)
-```
-
-or, to make a vector
-
-```
-unlist(lapply(X = l, FUN = mean))
-```
-
-or
-
-```
-sapply(X = l, FUN = mean)
-```
-
----
-
-# "Advanced" lapply
-
-Can "pick up" nontrivial list entries
-
-```
-l = list()
-for (i in 1:10) {
- l[[i]] = list()
- l[[i]]$a = runif(i)
- l[[i]]$b = runif(2*i)
-}
-sapply(X = l, FUN = function(x) length(x$b))
-```
-
-gives
-
-```
-[1] 2 4 6 8 10 12 14 16 18 20
-```
-
-Just recall: the argument to the function you define is a list entry (`l[[1]]`, `l[[2]]`, etc., here)
-
----
-
-# Avoid parameter variation loops with expand.grid
-
-```
-# Suppose we want to vary 3 parameters
-variations = list(
- p1 = seq(1, 10, length.out = 10),
- p2 = seq(0, 1, length.out = 10),
- p3 = seq(-1, 1, length.out = 10)
-)
-
-# Create the list
-tmp = expand.grid(variations)
-PARAMS = list()
-for (i in 1:dim(tmp)[1]) {
- PARAMS[[i]] = list()
- for (k in 1:length(variations)) {
- PARAMS[[i]][[names(variations)[k]]] = tmp[i, k]
- }
-}
-```
-
-There is still a loop, but you can split this list, use it on different machines, etc. And can use `parLapply`
-
----
-
-
-# Dealing with data
-
-- Example: population of South Africa
-- Example - Dutch Elm Disease
-- Data wrangling
-
-
-
-
-- JA. [Mathematical epidemiology in a data-rich world](http://dx.doi.org/10.1016/j.idm.2019.12.008). *Infectious Disease Modelling* **5**:161-188 (2020)
-- See also [GitHub repo](https://github.com/julien-arino/modelling-with-data) for that paper
-
-
-
----
-
-# It is important to be "data aware"
-
-- Using R (or Python), it is really easy to grab data from the web, e.g., from Open Data sources
-- More and more locations have an open data policy
-- As a modeller, you do not need to have data everywhere, but you should be aware of the context
-- If you want your work to have an impact, for instance in public health, you cannot be completely disconnected from reality
-
----
-
-# Data is everywhere
-
-## Closed data
-
-- Often generated by companies, governments or research labs
-- When available, come with multiple restrictions
-
-## Open data
-
-- Often generated by the same entities but "liberated" after a certain period
-- More and more frequent with governments/public entities
-- Wide variety of licenses, so beware
-- Wide variety of qualities, so beware
-
----
-
-# Open Data initiatives
-
-Recent movement (5-10 years): governments (local or higher) create portals where data are centralised and published
-
-- [Winnipeg](https://data.winnipeg.ca/)
-- [Alberta](https://open.alberta.ca/opendata)
-- [Canada](https://open.canada.ca/en/open-data)
-- [Europe](https://data.europa.eu/euodp/data/)
-- [UN](http://data.un.org/)
-- [World Bank](https://data.worldbank.org/)
-- [WHO](https://www.who.int/gho/database/en/)
-
----
-
-# Data gathering methods
-
-- By hand
-- Using programs such as [Engauge Digitizer](http://markummitchell.github.io/engauge-digitizer/) or [g3data](https://github.com/pn2200/g3data)
-- Using APIs
-- Using natural language processing and other web scraping methods
-- Using R or Python packages
-
----
-
-
-# Example: population of South Africa
-
----
-
-```
-library(wbstats)
-pop_data_CTRY <- wb_data(country = "ZAF", indicator = "SP.POP.TOTL",
- mrv = 100, return_wide = FALSE)
-y_range = range(pop_data_CTRY$value)
-y_axis <- make_y_axis(y_range)
-png(file = "pop_ZAF.png",
- width = 800, height = 400)
-plot(pop_data_CTRY$date, pop_data_CTRY$value * y_axis$factor,
- xlab = "Year", ylab = "Population", type = "b", lwd = 2,
- yaxt = "n")
-axis(2, at = y_axis$ticks, labels = y_axis$labels, las = 1)
-dev.off()
-crop_figure("pop_ZAF.png")
-```
-
----
-
-
-
----
-
-
-# Example - Dutch Elm Disease
-
----
-# Dutch Elm Disease
-
-- Fungal disease that affects Elms
-- Caused by the fungus *Ophiostoma ulmi*
-- Transmitted by the Elm bark beetle (*Scolytus scolytus*)
-- Has decimated North American urban elm forests
-
----
-
-
-
----
-
-
-
----
-
-
-
----
-
-# Getting the tree data
-
-```
-allTrees = read.csv("https://data.winnipeg.ca/api/views/hfwk-jp4h/ro
-```
-
-After this,
-
-```
-dim(allTrees)
-## [1] 300846
-15
-```
-
----
-
-# Let us clean things a little
-
-```
-elms_idx = grep("American Elm", allTrees$Common.Name, ignore.case = TRUE)
-elms = allTrees[elms_idx, ]
-```
-
-We are left with 54,036 American elms
-
----
-
-
-
----
-
-
-
----
-
-# Computation of root systems interactions
-
-(Needs a relatively large machine here - about 50GB RAM)
-
-- If roots of an infected tree touch roots of a susceptible tree, fungus is transmitted
-- Spread of a tree's root system depends on its height (we have diametre at breast height, DBH, for all trees)
-- The way roadways are built, there cannot be contacts between root systems of trees on opposite sides of a street
-
----
-
-# Distances between all trees
-
-```
-elms_xy = cbind(elms$X, elms$Y)
-D = dist(elms_xy)
-idx_D = which(D<50)
-```
-
-`indices_LT` is a large $N(N-1)/2\times 2$ matrix with indices (orig,dest) of trees in the pairs of elms, so `indices_LT[idx_D]` are the pairs under consideration
-
-Keep a little more..
-
-```
-indices_LT_kept = as.data.frame(cbind(indices_LT[idx_D,],
- D[idx_D]))
-colnames(indices_LT_kept) = c("i","j","dist")
-```
-
----
-
-# Create line segments between all pairs of trees
-
-```
-tree_locs_orig = cbind(elms_latlon$lon[indices_LT_kept$i],
- elms_latlon$lat[indices_LT_kept$i])
-tree_locs_dest = cbind(elms_latlon$lon[indices_LT_kept$j],
- elms_latlon$lat[indices_LT_kept$j])
-tree_pairs = do.call(
- sf::st_sfc,
- lapply(
- 1:nrow(tree_locs_orig),
- function(i){
- sf::st_linestring(
- matrix(
- c(tree_locs_orig[i,],
- tree_locs_dest[i,]),
- ncol=2,
- byrow=TRUE)
- )
- }
- )
-)
-```
-
----
-
-# A bit of mapping
-
-```
-library(tidyverse)
-# Get bounding polygon for Winnipeg
-bb_poly = osmdata::getbb(place_name = "winnipeg",
- format_out = "polygon")
-# Get roads
-roads <- osmdata::opq(bbox = bb_poly) %>%
- osmdata::add_osm_feature(key = 'highway',
- value = 'residential') %>%
- osmdata::osmdata_sf () %>%
- osmdata::trim_osmdata (bb_poly)
-# Get rivers
-rivers <- osmdata::opq(bbox = bb_poly) %>%
- osmdata::add_osm_feature(key = 'waterway',
- value = "river") %>%
- osmdata::osmdata_sf () %>%
- osmdata::trim_osmdata (bb_poly)
-```
-
----
-
-# And we finish easily
-
-- We have the pairs of trees potentially in contact with each other
-- We have the roads and rivers of the city, which is a collection of line segments
-- If there is an intersection between a tree pair and a road/river, then we can forget this tree pair as their root systems cannot come into contact
-
-```
-st_crs(tree_pairs) = sf::st_crs(roads$osm_lines$geometry)
-iroads = sf::st_intersects(x = roads$osm_lines$geometry,
- y = tree_pairs)
-irivers = sf::st_intersects(x = rivers$osm_lines$geometry,
- y = tree_pairs)
-```
-
----
-
-```
-tree_pairs_roads_intersect = c()
-for (i in 1:length(iroads)) {
- if (length(iroads[[i]])>0) {
- tree_pairs_roads_intersect = c(tree_pairs_roads_intersect,
- iroads[[i]])
- }
-}
-tree_pairs_roads_intersect = sort(tree_pairs_roads_intersect)
-to_keep = 1:dim(tree_locs_orig)[1]
-to_keep = setdiff(to_keep,tree_pairs_roads_intersect)
-```
-
----
-
-
-
----
-
-
-# Data wrangling
-
----
-
-# Data wrangling: `dplyr` vs `sqldf`
-
-`dplyr` is part of the `tidyverse` set of libraries. Load `magrittr` and its pipe `%>%`
-
-`sqldf` allows to use SQL on dataframes.. interesting alternative if you know SQL
-
----
-
-```
-library(sqldf)
-library(dplyr)
-
-SARS = read.csv("../DATA/SARS-CoV-1_data.csv")
-
-## Three ways to keep only the data for one country
-ctry = "Canada"
-# The basic one
-idx = which(SARS$country == ctry)
-SARS_selected = SARS[idx,]
-# The sqldf way
-SARS_selected = sqldf(paste0("SELECT * FROM SARS WHERE country = '",
- ctry, "'"))
-# The dplyr way
-SARS_selected = SARS %>%
- filter(country == ctry)
-```
-
----
-
-```
-# Create incidence for the selected country. diff does difference one by one,
-# so one less entry than the vector on which it is being used, thus we pad with a 0.
-SARS_selected$incidence = c(0, diff(SARS_selected$totalNumberCases))
-# Keep only positive incidences (discard 0 or negative adjustments)
-SARS_selected = SARS_selected %>%
- filter(incidence > 0)
-
-# Plot the result
-# Before plotting, we need to make the dates column we will use be actual dates..
-SARS_selected$toDate = lubridate::ymd(SARS_selected$toDate)
-EpiCurve(SARS_selected,
- date = "toDate", period = "day",
- freq = "incidence",
- title = "SARS-CoV-1 incidence in Canada in 2003")
-```
-
----
-
-
-
----
-
-
-# Solving ODE numerically
-
-- The deSolve library
-- Example - Fitting data
-
----
-
-
-# The deSolve library
-
----
-
-# The deSolve library
-
-- As I have already pointed out, [`deSolve`](https://cran.r-project.org/web/packages/deSolve/index.html):
-> The functions provide an interface to the FORTRAN functions 'lsoda', 'lsodar', 'lsode', 'lsodes' of the 'ODEPACK' collection, to the FORTRAN functions 'dvode', 'zvode' and 'daspk' and a C-implementation of solvers of the 'Runge-Kutta' family with fixed or variable time steps
-
-- So you are benefiting from years and year of experience: [ODEPACK](https://computing.llnl.gov/projects/odepack) is a set of Fortran (77!) solvers developed at Lawrence Livermore National Laboratory (LLNL) starting in the late 70s
-
-- Other good solvers are also included, those written in C
-
-- Refer to the [package help](https://cran.r-project.org/web/packages/deSolve/deSolve.pdf) for details
-
----
-
-# Using deSolve for simple ODEs
-
-As with more numerical solvers, you need to write a function returning the value of the right hand side of your equation (the vector field) at a given point in phase space, then call this function from the solver
-
-```
-library(deSolve)
-rhs_logistic <- function(t, x, p) {
- with(as.list(x), {
- dN <- p$r * N *(1-N/p$K)
- return(list(dN))
- })
-}
-params = list(r = 0.1, K = 100)
-IC = c(N = 50)
-times = seq(0, 100, 1)
-sol <- ode(IC, times, rhs_logistic, params)
-```
-
----
-
-This also works: add `p` to arguments of `as.list` and thus use without `p$` prefix
-
-```
-library(deSolve)
-rhs_logistic <- function(t, x, p) {
- with(as.list(c(x, p)), {
- dN <- r * N *(1-N/K)
- return(list(dN))
- })
-}
-params = list(r = 0.1, K = 100)
-IC = c(N = 50)
-times = seq(0, 100, 1)
-sol <- ode(IC, times, rhs_logistic, params)
-```
-
-In this case, beware of not having a variable and a parameter with the same name..
-
----
-
-# Default method: `lsoda`
-
-- `lsoda` switches automatically between stiff and nonstiff methods
-
-- You can also specify other methods: "lsode", "lsodes", "lsodar", "vode", "daspk", "euler", "rk4", "ode23", "ode45", "radau", "bdf", "bdf_d", "adams", "impAdams" or "impAdams_d" ,"iteration" (the latter for discrete-time systems)
-
-```
-ode(y, times, func, parms,
- method = "ode45")
-```
-
-- You can even implement your own integration method
-
----
-
-
-# Example - Fitting data
-
----
-
-# Example - Fitting data
-
-- Note that this is a super simplified version of what to do
-- Much more elaborate procedures exist
- - Roda. [Bayesian inference for dynamical systems](https://doi.org/10.1016/j.idm.2019.12.007)
- - Portet. [A primer on model selection using the Akaike Information Criterion](https://doi.org/10.1016/j.idm.2019.12.010)
-- Let us grab some epi data online and fit an SIR model to it
-- Don't expect anything funky, as I said, this is the baby version
-- Also, keep in mind that any identification procedure is subject to risks due to *identifiability issues*; see, e.g., Roda et al, [Why is it difficult to accurately predict the COVID-19 epidemic?](https://doi.org/10.1016/j.idm.2020.03.001)
-
----
-
-# Principle
-
-- Data is a set $(t_i,y_i)$, $i=1,\ldots,N$, where $t_i\in\mathcal{I}$, some interval
-- Solution to SIR is $(t,x(t))$ for $t\in\mathcal{I}$
-- Suppose parameters of the model are $p$
-- We want to minimise the error function
-$$
-E(p) = \sum_{i=1}^N \|x(t_i)-y_i\|
-$$
-- Norm is typically Euclidean, but could be different depending on objectives
-- So given a point $p$ in (admissible) parameter space, we compute the solution to the ODE, compute $E(p)$
-- Using some minimisation algorithm, we seek a minimum of $E(p)$ by varying $p$
-
----
-
-# What are $y_i$ and $x(t_i)$ here?
-
-- In epi data for infectious diseases, we typically have incidence, i.e., number of new cases per unit time
-- In SIR model, this is $\beta SI$ or $\beta SI/N$, so, if using mass action incidence and Euclidean norm
-$$
-E(p)=\sum_{i=1}^N(\beta S(t_i)I(t_i)-y_i)^2
-$$
-or, if using standard incidence
-$$
-E(p)=\sum_{i=1}^N
-\left(\beta \frac{S(t_i)I(t_i)}{N}-y_i\right)^2
-$$
-
----
-
-# Implementing in practice
-
-See the code [practicum_01_fitting.R](https://raw.githubusercontent.com/julien-arino/3MC-course-epidemiological-modelling/main/CODE/practicum_01_fitting.R), which we will go over now
\ No newline at end of file
diff --git a/SLIDES/vignette-01-introduction-installation.html b/SLIDES/vignette-01-introduction-installation.html
new file mode 100644
index 0000000..bf01d1e
--- /dev/null
+++ b/SLIDES/vignette-01-introduction-installation.html
@@ -0,0 +1,93 @@
+Vignette 01 - Introduction to R. Installing R
\ No newline at end of file
diff --git a/SLIDES/vignette-01-introduction-installation.md b/SLIDES/vignette-01-introduction-installation.md
new file mode 100644
index 0000000..45fffa6
--- /dev/null
+++ b/SLIDES/vignette-01-introduction-installation.md
@@ -0,0 +1,114 @@
+---
+marp: true
+title: Vignette 01 - Introduction to R. Installing R
+description: Julien Arino - R for modellers - Vignette 01 - Introduction to R. Installing R.
+theme: default
+class: invert
+math: mathjax
+paginate: false
+size: 4:3
+---
+
+
+
+
+# Vignette 01 - Introduction to R. Installing R
+
+Julien Arino [](mailto:Julien.Arino@umanitoba.ca) [](https://julien-arino.github.io/) [](https://github.com/julien-arino)
+
+Department of Mathematics & Data Science Nexus
+University of Manitoba*
+
+
+
+Canadian Centre for Disease Modelling
+
+
+* The University of Manitoba campuses are located on original lands of Anishinaabeg, Cree, Oji-Cree, Dakota and Dene peoples, and on the homeland of the Métis Nation.
+
+---
+
+
+# Outline
+
+- Foreword: the R language
+- Programming in R
+
+---
+
+
+# Foreword: the R language
+
+---
+
+# R was originally for stats but is now much more
+
+- Open source version of S
+- Appeared in 1993
+- Now (2024-01) version 4.3
+- One major advantage in my view: uses a lot of C and Fortran code. E.g., `deSolve`:
+> The functions provide an interface to the FORTRAN functions 'lsoda', 'lsodar', 'lsode', 'lsodes' of the 'ODEPACK' collection, to the FORTRAN functions 'dvode', 'zvode' and 'daspk' and a C-implementation of solvers of the 'Runge-Kutta' family with fixed or variable time steps
+- Very active community on the web, easy to find solutions (same true of Python, I just prefer R)
+
+---
+
+# Development environments
+
+- Terminal version, not very friendly
+- Nicer terminal: [radian](https://github.com/randy3k/radian)
+- Execute R scripts by using `Rscript name_of_script.R`. Useful to run code in `cron`, for instance
+- Use IDEs:
+ - [RStudio](https://www.rstudio.com/products/rstudio/) has become the reference
+ - [RKWard](https://invent.kde.org/education/rkward) is useful if you are for instance using an ARM processor (Raspberry Pi, some Chromebooks..)
+- Integrate into jupyter notebooks
+
+---
+
+# Going further
+
+- [RStudio server](https://www.rstudio.com/products/rstudio/#rstudio-server): run RStudio on a Linux server and connect via a web interface
+- Shiny: easily create an interactive web site running R code
+- [Shiny server](https://www.rstudio.com/products/shiny/shiny-server/): run Shiny apps on a Linux server
+- Rmarkdown: markdown that incorporates R commands. Useful for generating reports in html or pdf, can make slides as well..
+- RSweave: LaTeX incorporating R commands. Useful for generating reports. Not used as much as Rmarkdown these days
+
+---
+
+# R is a scripted language
+
+- Interactive
+- Allows you to work in real time
+ - Be careful: what is in memory might involve steps not written down in a script
+ - If you want to reproduce your steps, it is good to write all the steps down in a script and to test from time to time running using `Rscript`: this will ensure that all that is required to run is indeed loaded to memory when it needs to, i.e., that it is not already there..
+
+---
+
+# Similar to matlab..
+
+.. with some differences, of course! Otherwise, where would the fun be? ;)
+
+---
+
+
+# Installing `R`
+
diff --git a/SLIDES/vignette-02-Rstudio-and-friends.html b/SLIDES/vignette-02-Rstudio-and-friends.html
new file mode 100644
index 0000000..35e99b5
--- /dev/null
+++ b/SLIDES/vignette-02-Rstudio-and-friends.html
@@ -0,0 +1,58 @@
+Vignette 02 - RStudio and friends
\ No newline at end of file
diff --git a/SLIDES/vignette-02-Rstudio-and-friends.md b/SLIDES/vignette-02-Rstudio-and-friends.md
new file mode 100644
index 0000000..08f3410
--- /dev/null
+++ b/SLIDES/vignette-02-Rstudio-and-friends.md
@@ -0,0 +1,82 @@
+---
+marp: true
+title: Vignette 02 - RStudio and friends
+description: Julien Arino - R for modellers - Vignette 02 - RStudio and friends.
+theme: default
+class: invert
+math: mathjax
+paginate: false
+size: 4:3
+---
+
+
+
+
+# Vignette 02 - RStudio and friends
+
+Julien Arino [](mailto:Julien.Arino@umanitoba.ca) [](https://julien-arino.github.io/) [](https://github.com/julien-arino)
+
+Department of Mathematics
+University of Manitoba*
+
+
+
+Canadian Centre for Disease Modelling
+
+
+* The University of Manitoba campuses are located on original lands of Anishinaabeg, Cree, Oji-Cree, Dakota and Dene peoples, and on the homeland of the Métis Nation.
+
+---
+
+
+# Outline
+
+- Foreword: the R language
+- Programming in R
+- Dealing with data
+- Solving ODE numerically
+
+---
+
+
+# Foreword: the R language
+
+---
+
+# Development environments
+
+- Use IDEs:
+ - [RStudio](https://www.rstudio.com/products/rstudio/) has become the reference
+ - [RKWard](https://invent.kde.org/education/rkward) is useful if you are for instance using an ARM processor (Raspberry Pi, some Chromebooks..)
+- Integrate into jupyter notebooks
+
+---
+
+# Going further
+
+- [RStudio server](https://www.rstudio.com/products/rstudio/#rstudio-server): run RStudio on a Linux server and connect via a web interface
+- Shiny: easily create an interactive web site running R code
+- [Shiny server](https://www.rstudio.com/products/shiny/shiny-server/): run Shiny apps on a Linux server
+- Rmarkdown: markdown that incorporates R commands. Useful for generating reports in html or pdf, can make slides as well..
+- RSweave: LaTeX incorporating R commands. Useful for generating reports. Not used as much as Rmarkdown these days
+
diff --git a/SLIDES/vignette-03-installing-using-packages.md b/SLIDES/vignette-03-installing-using-packages.md
new file mode 100644
index 0000000..f9265a7
--- /dev/null
+++ b/SLIDES/vignette-03-installing-using-packages.md
@@ -0,0 +1,94 @@
+---
+marp: true
+title: Vignette 03 - Installing and loading packages
+description: Julien Arino - R for modellers - Vignette 03 - Installing and loading packages.
+theme: default
+class: invert
+math: mathjax
+paginate: false
+size: 4:3
+---
+
+
+
+
+# Vignette 03 - Installing and loading packages
+
+Julien Arino [](mailto:Julien.Arino@umanitoba.ca) [](https://julien-arino.github.io/) [](https://github.com/julien-arino)
+
+Department of Mathematics
+University of Manitoba*
+
+
+
+Canadian Centre for Disease Modelling
+
+
+* The University of Manitoba campuses are located on original lands of Anishinaabeg, Cree, Oji-Cree, Dakota and Dene peoples, and on the homeland of the Métis Nation.
+
+---
+
+# Note - Required reading/watching for MATH 2740 students
+
+If you are a student in the University of Manitoba's Mathematics of Data Science course (MATH 2740), this is **required** reading/watching
+
+Failure to use the "user friendly" method presented later will result in loss of marks in your `R` assignments!
+
+---
+
+
+# Outline
+
+- Packages (a.k.a. libraries)
+- Installing a package
+- Loading a package
+- Be friendly to others!
+
+---
+
+
+# Packages (a.k.a. libraries)
+
+---
+
+# Be friendly to others!
+
+---
+
+# When distributing your code, think of those using it
+
+If you are using a slightly unusual library, it is possible that a person you share your code with does not have that library installed
+
+In this case, it is nice to them if you spare them having to do the work to install the library
+
+But it is also possible that they already have the library
+
+In this case, it will be annoying to them if you trigger an installation of the library (especially under linux, since there libraries are compiled for installation)
+
+---
+
+So the way to proceed is to test whether the library is installed
+
+If it is, load it
+
+If it is not, install it then load it
\ No newline at end of file
diff --git a/SLIDES/vignette-04-data-types.md b/SLIDES/vignette-04-data-types.md
new file mode 100644
index 0000000..bd34ed7
--- /dev/null
+++ b/SLIDES/vignette-04-data-types.md
@@ -0,0 +1,818 @@
+---
+marp: true
+title: Vignette 04 - Data types
+description: Julien Arino - R for modellers - Vignette 04 - Data types.
+theme: default
+class: invert
+math: mathjax
+paginate: false
+size: 4:3
+---
+
+
+
+
+# Lecture 01 - Introduction to R. Installing R
+
+Julien Arino [](mailto:Julien.Arino@umanitoba.ca) [](https://julien-arino.github.io/) [](https://github.com/julien-arino)
+
+Department of Mathematics
+University of Manitoba*
+
+
+
+Canadian Centre for Disease Modelling
+
+
+* The University of Manitoba campuses are located on original lands of Anishinaabeg, Cree, Oji-Cree, Dakota and Dene peoples, and on the homeland of the Métis Nation.
+
+---
+
+
+# Outline
+
+- Foreword: the R language
+- Programming in R
+- Dealing with data
+- Solving ODE numerically
+
+---
+
+
+# Foreword: the R language
+
+---
+
+# R was originally for stats but is now more
+
+- Open source version of S
+- Appeared in 1993
+- Now version 4.2
+- One major advantage in my view: uses a lot of C and Fortran code. E.g., `deSolve`:
+> The functions provide an interface to the FORTRAN functions 'lsoda', 'lsodar', 'lsode', 'lsodes' of the 'ODEPACK' collection, to the FORTRAN functions 'dvode', 'zvode' and 'daspk' and a C-implementation of solvers of the 'Runge-Kutta' family with fixed or variable time steps
+- Very active community on the web, easy to find solutions (same true of Python, I just prefer R)
+
+---
+
+# Development environments
+
+- Terminal version, not very friendly
+- Nicer terminal: [radian](https://github.com/randy3k/radian)
+- Execute R scripts by using `Rscript name_of_script.R`. Useful to run code in `cron`, for instance
+- Use IDEs:
+ - [RStudio](https://www.rstudio.com/products/rstudio/) has become the reference
+ - [RKWard](https://invent.kde.org/education/rkward) is useful if you are for instance using an ARM processor (Raspberry Pi, some Chromebooks..)
+- Integrate into jupyter notebooks
+
+---
+
+# Going further
+
+- [RStudio server](https://www.rstudio.com/products/rstudio/#rstudio-server): run RStudio on a Linux server and connect via a web interface
+- Shiny: easily create an interactive web site running R code
+- [Shiny server](https://www.rstudio.com/products/shiny/shiny-server/): run Shiny apps on a Linux server
+- Rmarkdown: markdown that incorporates R commands. Useful for generating reports in html or pdf, can make slides as well..
+- RSweave: LaTeX incorporating R commands. Useful for generating reports. Not used as much as Rmarkdown these days
+
+---
+
+# R is a scripted language
+
+- Interactive
+- Allows you to work in real time
+ - Be careful: what is in memory might involve steps not written down in a script
+ - If you want to reproduce your steps, it is good to write all the steps down in a script and to test from time to time running using `Rscript`: this will ensure that all that is required to run is indeed loaded to memory when it needs to, i.e., that it is not already there..
+
+---
+
+
+# Programming in R
+
+---
+
+# Similar to matlab..
+
+.. with some differences, of course! Otherwise, where would the fun be? ;)
+
+---
+
+# Assignment
+
+Two ways:
+
+```
+X <- 10
+```
+
+or
+
+```
+X = 10
+```
+
+First version is preferred by R purists.. I don't really care
+
+---
+
+# Lists
+
+A very useful data structure, quite flexible and versatile. Empty list: `L <- list()`. Convenient for things like parameters. For instance
+
+```
+L <- list()
+L$a <- 10
+L$b <- 3
+L[["another_name"]] <- "Plouf plouf"
+```
+
+```
+> L[1]
+$a
+[1] 10
+> L[[2]]
+[1] 3
+> L$a
+[1] 10
+> L[["b"]]
+[1] 3
+> L$another_name
+[1] "Plouf plouf"
+```
+
+---
+
+# Vectors
+
+```
+x = 1:10
+y <- c(x, 12)
+> y
+ [1] 1 2 3 4 5 6 7 8 9 10 12
+z = c("red", "blue")
+> z
+[1] "red" "blue"
+z = c(z, 1)
+> z
+[1] "red" "blue" "1"
+```
+Note that in `z`, since the first two entries are characters, the added entry is also a character. Contrary to lists, vectors have all entries of the same type
+
+---
+
+# Matrices
+
+Matrix (or vector) of zeros
+```
+A <- mat.or.vec(nr = 2, nc = 3)
+```
+
+Matrix with prescribed entries
+
+```
+B <- matrix(c(1,2,3,4), nr = 2, nc = 2)
+> B
+ [,1] [,2]
+[1,] 1 3
+[2,] 2 4
+C <- matrix(c(1,2,3,4), nr = 2, nc = 2, byrow = TRUE)
+> C
+ [,1] [,2]
+[1,] 1 2
+[2,] 3 4
+```
+
+Remark that here and elsewhere, naming the arguments (e.g., `nr = 2`) allows to use arguments in any order
+
+---
+
+# Matrix operations
+
+Probably the biggest annoyance in R compared to other languages
+
+- The notation `A*B` is the *Hadamard product* $A\circ B$ (what would be denoted `A.*B` in matlab), not the standard matrix multiplication
+- Matrix multiplication is written `A %*% B`
+
+---
+
+# Vector operations
+
+Vector addition is also frustrating. Say you write `x=1:10`, i.e., make the vector
+```
+> x
+ [1] 1 2 3 4 5 6 7 8 9 10
+```
+Then `x+1` gives
+```
+> x+1
+ [1] 2 3 4 5 6 7 8 9 10 11
+ ```
+ i.e., adds 1 to all entries in the vector
+
+ Beware of this in particular when addressing sets of indices in lists, vectors or matrices
+
+---
+
+# For the matlab-ers here
+
+- R does not have the keyword `end` to access the last entry in a matrix/vector/list..
+- Use `length` (lists or vectors), `nchar` (character chains), `dim` (matrices.. careful, of course returns 2 values)
+
+---
+
+# Flow control
+
+```
+if (condition is true) {
+ list of stuff to do
+}
+```
+
+Even if `list of stuff to do` is a single instruction, best to use curly braces
+
+```
+if (condition is true) {
+ list of stuff to do
+} else if (another condition) {
+ ...
+} else {
+ ...
+}
+```
+
+---
+
+# For loops
+
+`for` applies to lists or vectors
+
+```
+for (i in 1:10) {
+ something using integer i
+}
+for (j in c(1,3,4)) {
+ something using integer j
+}
+for (n in c("truc", "muche", "chose")) {
+ something using string n
+}
+for (m in list("truc", "muche", "chose", 1, 2)) {
+ something using string n or integer n, depending
+}
+```
+
+---
+
+# lapply
+
+Very useful function (a few others in the same spirit: `sapply`, `vapply`, `mapply`)
+
+Applies a function to each entry in a list/vector/matrix
+
+Because there is a parallel version (`parLapply`) that we will see later, worth learning
+
+```
+l = list()
+for (i in 1:10) {
+ l[[i]] = runif(i)
+}
+lapply(X = l, FUN = mean)
+```
+
+or, to make a vector
+
+```
+unlist(lapply(X = l, FUN = mean))
+```
+
+or
+
+```
+sapply(X = l, FUN = mean)
+```
+
+---
+
+# "Advanced" lapply
+
+Can "pick up" nontrivial list entries
+
+```
+l = list()
+for (i in 1:10) {
+ l[[i]] = list()
+ l[[i]]$a = runif(i)
+ l[[i]]$b = runif(2*i)
+}
+sapply(X = l, FUN = function(x) length(x$b))
+```
+
+gives
+
+```
+[1] 2 4 6 8 10 12 14 16 18 20
+```
+
+Just recall: the argument to the function you define is a list entry (`l[[1]]`, `l[[2]]`, etc., here)
+
+---
+
+# Avoid parameter variation loops with expand.grid
+
+```
+# Suppose we want to vary 3 parameters
+variations = list(
+ p1 = seq(1, 10, length.out = 10),
+ p2 = seq(0, 1, length.out = 10),
+ p3 = seq(-1, 1, length.out = 10)
+)
+
+# Create the list
+tmp = expand.grid(variations)
+PARAMS = list()
+for (i in 1:dim(tmp)[1]) {
+ PARAMS[[i]] = list()
+ for (k in 1:length(variations)) {
+ PARAMS[[i]][[names(variations)[k]]] = tmp[i, k]
+ }
+}
+```
+
+There is still a loop, but you can split this list, use it on different machines, etc. And can use `parLapply`
+
+---
+
+
+# Dealing with data
+
+- Example: population of South Africa
+- Example - Dutch Elm Disease
+- Data wrangling
+
+
+
+
+- JA. [Mathematical epidemiology in a data-rich world](http://dx.doi.org/10.1016/j.idm.2019.12.008). *Infectious Disease Modelling* **5**:161-188 (2020)
+- See also [GitHub repo](https://github.com/julien-arino/modelling-with-data) for that paper
+
+
+
+---
+
+# It is important to be "data aware"
+
+- Using R (or Python), it is really easy to grab data from the web, e.g., from Open Data sources
+- More and more locations have an open data policy
+- As a modeller, you do not need to have data everywhere, but you should be aware of the context
+- If you want your work to have an impact, for instance in public health, you cannot be completely disconnected from reality
+
+---
+
+# Data is everywhere
+
+## Closed data
+
+- Often generated by companies, governments or research labs
+- When available, come with multiple restrictions
+
+## Open data
+
+- Often generated by the same entities but "liberated" after a certain period
+- More and more frequent with governments/public entities
+- Wide variety of licenses, so beware
+- Wide variety of qualities, so beware
+
+---
+
+# Open Data initiatives
+
+Recent movement (5-10 years): governments (local or higher) create portals where data are centralised and published
+
+- [Winnipeg](https://data.winnipeg.ca/)
+- [Alberta](https://open.alberta.ca/opendata)
+- [Canada](https://open.canada.ca/en/open-data)
+- [Europe](https://data.europa.eu/euodp/data/)
+- [UN](http://data.un.org/)
+- [World Bank](https://data.worldbank.org/)
+- [WHO](https://www.who.int/gho/database/en/)
+
+---
+
+# Data gathering methods
+
+- By hand
+- Using programs such as [Engauge Digitizer](http://markummitchell.github.io/engauge-digitizer/) or [g3data](https://github.com/pn2200/g3data)
+- Using APIs
+- Using natural language processing and other web scraping methods
+- Using R or Python packages
+
+---
+
+
+# Example: population of South Africa
+
+---
+
+```
+library(wbstats)
+pop_data_CTRY <- wb_data(country = "ZAF", indicator = "SP.POP.TOTL",
+ mrv = 100, return_wide = FALSE)
+y_range = range(pop_data_CTRY$value)
+y_axis <- make_y_axis(y_range)
+png(file = "pop_ZAF.png",
+ width = 800, height = 400)
+plot(pop_data_CTRY$date, pop_data_CTRY$value * y_axis$factor,
+ xlab = "Year", ylab = "Population", type = "b", lwd = 2,
+ yaxt = "n")
+axis(2, at = y_axis$ticks, labels = y_axis$labels, las = 1)
+dev.off()
+crop_figure("pop_ZAF.png")
+```
+
+---
+
+
+
+---
+
+
+# Example - Dutch Elm Disease
+
+---
+# Dutch Elm Disease
+
+- Fungal disease that affects Elms
+- Caused by the fungus *Ophiostoma ulmi*
+- Transmitted by the Elm bark beetle (*Scolytus scolytus*)
+- Has decimated North American urban elm forests
+
+---
+
+
+
+---
+
+
+
+---
+
+
+
+---
+
+# Getting the tree data
+
+```
+allTrees = read.csv("https://data.winnipeg.ca/api/views/hfwk-jp4h/ro
+```
+
+After this,
+
+```
+dim(allTrees)
+## [1] 300846
+15
+```
+
+---
+
+# Let us clean things a little
+
+```
+elms_idx = grep("American Elm", allTrees$Common.Name, ignore.case = TRUE)
+elms = allTrees[elms_idx, ]
+```
+
+We are left with 54,036 American elms
+
+---
+
+
+
+---
+
+
+
+---
+
+# Computation of root systems interactions
+
+(Needs a relatively large machine here - about 50GB RAM)
+
+- If roots of an infected tree touch roots of a susceptible tree, fungus is transmitted
+- Spread of a tree's root system depends on its height (we have diametre at breast height, DBH, for all trees)
+- The way roadways are built, there cannot be contacts between root systems of trees on opposite sides of a street
+
+---
+
+# Distances between all trees
+
+```
+elms_xy = cbind(elms$X, elms$Y)
+D = dist(elms_xy)
+idx_D = which(D<50)
+```
+
+`indices_LT` is a large $N(N-1)/2\times 2$ matrix with indices (orig,dest) of trees in the pairs of elms, so `indices_LT[idx_D]` are the pairs under consideration
+
+Keep a little more..
+
+```
+indices_LT_kept = as.data.frame(cbind(indices_LT[idx_D,],
+ D[idx_D]))
+colnames(indices_LT_kept) = c("i","j","dist")
+```
+
+---
+
+# Create line segments between all pairs of trees
+
+```
+tree_locs_orig = cbind(elms_latlon$lon[indices_LT_kept$i],
+ elms_latlon$lat[indices_LT_kept$i])
+tree_locs_dest = cbind(elms_latlon$lon[indices_LT_kept$j],
+ elms_latlon$lat[indices_LT_kept$j])
+tree_pairs = do.call(
+ sf::st_sfc,
+ lapply(
+ 1:nrow(tree_locs_orig),
+ function(i){
+ sf::st_linestring(
+ matrix(
+ c(tree_locs_orig[i,],
+ tree_locs_dest[i,]),
+ ncol=2,
+ byrow=TRUE)
+ )
+ }
+ )
+)
+```
+
+---
+
+# A bit of mapping
+
+```
+library(tidyverse)
+# Get bounding polygon for Winnipeg
+bb_poly = osmdata::getbb(place_name = "winnipeg",
+ format_out = "polygon")
+# Get roads
+roads <- osmdata::opq(bbox = bb_poly) %>%
+ osmdata::add_osm_feature(key = 'highway',
+ value = 'residential') %>%
+ osmdata::osmdata_sf () %>%
+ osmdata::trim_osmdata (bb_poly)
+# Get rivers
+rivers <- osmdata::opq(bbox = bb_poly) %>%
+ osmdata::add_osm_feature(key = 'waterway',
+ value = "river") %>%
+ osmdata::osmdata_sf () %>%
+ osmdata::trim_osmdata (bb_poly)
+```
+
+---
+
+# And we finish easily
+
+- We have the pairs of trees potentially in contact with each other
+- We have the roads and rivers of the city, which is a collection of line segments
+- If there is an intersection between a tree pair and a road/river, then we can forget this tree pair as their root systems cannot come into contact
+
+```
+st_crs(tree_pairs) = sf::st_crs(roads$osm_lines$geometry)
+iroads = sf::st_intersects(x = roads$osm_lines$geometry,
+ y = tree_pairs)
+irivers = sf::st_intersects(x = rivers$osm_lines$geometry,
+ y = tree_pairs)
+```
+
+---
+
+```
+tree_pairs_roads_intersect = c()
+for (i in 1:length(iroads)) {
+ if (length(iroads[[i]])>0) {
+ tree_pairs_roads_intersect = c(tree_pairs_roads_intersect,
+ iroads[[i]])
+ }
+}
+tree_pairs_roads_intersect = sort(tree_pairs_roads_intersect)
+to_keep = 1:dim(tree_locs_orig)[1]
+to_keep = setdiff(to_keep,tree_pairs_roads_intersect)
+```
+
+---
+
+
+
+---
+
+
+# Data wrangling
+
+---
+
+# Data wrangling: `dplyr` vs `sqldf`
+
+`dplyr` is part of the `tidyverse` set of libraries. Load `magrittr` and its pipe `%>%`
+
+`sqldf` allows to use SQL on dataframes.. interesting alternative if you know SQL
+
+---
+
+```
+library(sqldf)
+library(dplyr)
+
+SARS = read.csv("../DATA/SARS-CoV-1_data.csv")
+
+## Three ways to keep only the data for one country
+ctry = "Canada"
+# The basic one
+idx = which(SARS$country == ctry)
+SARS_selected = SARS[idx,]
+# The sqldf way
+SARS_selected = sqldf(paste0("SELECT * FROM SARS WHERE country = '",
+ ctry, "'"))
+# The dplyr way
+SARS_selected = SARS %>%
+ filter(country == ctry)
+```
+
+---
+
+```
+# Create incidence for the selected country. diff does difference one by one,
+# so one less entry than the vector on which it is being used, thus we pad with a 0.
+SARS_selected$incidence = c(0, diff(SARS_selected$totalNumberCases))
+# Keep only positive incidences (discard 0 or negative adjustments)
+SARS_selected = SARS_selected %>%
+ filter(incidence > 0)
+
+# Plot the result
+# Before plotting, we need to make the dates column we will use be actual dates..
+SARS_selected$toDate = lubridate::ymd(SARS_selected$toDate)
+EpiCurve(SARS_selected,
+ date = "toDate", period = "day",
+ freq = "incidence",
+ title = "SARS-CoV-1 incidence in Canada in 2003")
+```
+
+---
+
+
+
+---
+
+
+# Solving ODE numerically
+
+- The deSolve library
+- Example - Fitting data
+
+---
+
+
+# The deSolve library
+
+---
+
+# The deSolve library
+
+- As I have already pointed out, [`deSolve`](https://cran.r-project.org/web/packages/deSolve/index.html):
+> The functions provide an interface to the FORTRAN functions 'lsoda', 'lsodar', 'lsode', 'lsodes' of the 'ODEPACK' collection, to the FORTRAN functions 'dvode', 'zvode' and 'daspk' and a C-implementation of solvers of the 'Runge-Kutta' family with fixed or variable time steps
+
+- So you are benefiting from years and year of experience: [ODEPACK](https://computing.llnl.gov/projects/odepack) is a set of Fortran (77!) solvers developed at Lawrence Livermore National Laboratory (LLNL) starting in the late 70s
+
+- Other good solvers are also included, those written in C
+
+- Refer to the [package help](https://cran.r-project.org/web/packages/deSolve/deSolve.pdf) for details
+
+---
+
+# Using deSolve for simple ODEs
+
+As with more numerical solvers, you need to write a function returning the value of the right hand side of your equation (the vector field) at a given point in phase space, then call this function from the solver
+
+```
+library(deSolve)
+rhs_logistic <- function(t, x, p) {
+ with(as.list(x), {
+ dN <- p$r * N *(1-N/p$K)
+ return(list(dN))
+ })
+}
+params = list(r = 0.1, K = 100)
+IC = c(N = 50)
+times = seq(0, 100, 1)
+sol <- ode(IC, times, rhs_logistic, params)
+```
+
+---
+
+This also works: add `p` to arguments of `as.list` and thus use without `p$` prefix
+
+```
+library(deSolve)
+rhs_logistic <- function(t, x, p) {
+ with(as.list(c(x, p)), {
+ dN <- r * N *(1-N/K)
+ return(list(dN))
+ })
+}
+params = list(r = 0.1, K = 100)
+IC = c(N = 50)
+times = seq(0, 100, 1)
+sol <- ode(IC, times, rhs_logistic, params)
+```
+
+In this case, beware of not having a variable and a parameter with the same name..
+
+---
+
+# Default method: `lsoda`
+
+- `lsoda` switches automatically between stiff and nonstiff methods
+
+- You can also specify other methods: "lsode", "lsodes", "lsodar", "vode", "daspk", "euler", "rk4", "ode23", "ode45", "radau", "bdf", "bdf_d", "adams", "impAdams" or "impAdams_d" ,"iteration" (the latter for discrete-time systems)
+
+```
+ode(y, times, func, parms,
+ method = "ode45")
+```
+
+- You can even implement your own integration method
+
+---
+
+
+# Example - Fitting data
+
+---
+
+# Example - Fitting data
+
+- Note that this is a super simplified version of what to do
+- Much more elaborate procedures exist
+ - Roda. [Bayesian inference for dynamical systems](https://doi.org/10.1016/j.idm.2019.12.007)
+ - Portet. [A primer on model selection using the Akaike Information Criterion](https://doi.org/10.1016/j.idm.2019.12.010)
+- Let us grab some epi data online and fit an SIR model to it
+- Don't expect anything funky, as I said, this is the baby version
+- Also, keep in mind that any identification procedure is subject to risks due to *identifiability issues*; see, e.g., Roda et al, [Why is it difficult to accurately predict the COVID-19 epidemic?](https://doi.org/10.1016/j.idm.2020.03.001)
+
+---
+
+# Principle
+
+- Data is a set $(t_i,y_i)$, $i=1,\ldots,N$, where $t_i\in\mathcal{I}$, some interval
+- Solution to SIR is $(t,x(t))$ for $t\in\mathcal{I}$
+- Suppose parameters of the model are $p$
+- We want to minimise the error function
+$$
+E(p) = \sum_{i=1}^N \|x(t_i)-y_i\|
+$$
+- Norm is typically Euclidean, but could be different depending on objectives
+- So given a point $p$ in (admissible) parameter space, we compute the solution to the ODE, compute $E(p)$
+- Using some minimisation algorithm, we seek a minimum of $E(p)$ by varying $p$
+
+---
+
+# What are $y_i$ and $x(t_i)$ here?
+
+- In epi data for infectious diseases, we typically have incidence, i.e., number of new cases per unit time
+- In SIR model, this is $\beta SI$ or $\beta SI/N$, so, if using mass action incidence and Euclidean norm
+$$
+E(p)=\sum_{i=1}^N(\beta S(t_i)I(t_i)-y_i)^2
+$$
+or, if using standard incidence
+$$
+E(p)=\sum_{i=1}^N
+\left(\beta \frac{S(t_i)I(t_i)}{N}-y_i\right)^2
+$$
+
+---
+
+# Implementing in practice
+
+See the code [practicum_01_fitting.R](https://raw.githubusercontent.com/julien-arino/3MC-course-epidemiological-modelling/main/CODE/practicum_01_fitting.R), which we will go over now
\ No newline at end of file
diff --git a/SLIDES/vignette-05-flow-control.html b/SLIDES/vignette-05-flow-control.html
new file mode 100644
index 0000000..67fb979
--- /dev/null
+++ b/SLIDES/vignette-05-flow-control.html
@@ -0,0 +1,63 @@
+Vignette 05 - Flow control
\ No newline at end of file
diff --git a/SLIDES/vignette-05-flow-control.md b/SLIDES/vignette-05-flow-control.md
new file mode 100644
index 0000000..3a525ed
--- /dev/null
+++ b/SLIDES/vignette-05-flow-control.md
@@ -0,0 +1,98 @@
+---
+marp: true
+title: Vignette 05 - Flow control
+description: Julien Arino - R for modellers - Vignette 05 - Flow control.
+theme: default
+class: invert
+math: mathjax
+paginate: false
+size: 4:3
+---
+
+
+
+
+# Vignette 05 - Flow control
+
+Julien Arino [](mailto:Julien.Arino@umanitoba.ca) [](https://julien-arino.github.io/) [](https://github.com/julien-arino)
+
+Department of Mathematics
+University of Manitoba*
+
+
+
+Canadian Centre for Disease Modelling
+
+
+* The University of Manitoba campuses are located on original lands of Anishinaabeg, Cree, Oji-Cree, Dakota and Dene peoples, and on the homeland of the Métis Nation.
+
+---
+
+
+# Outline
+
+-
+
+---
+
+# `if` statements
+
+```R
+if (condition is true) {
+ list of stuff to do
+}
+```
+
+Even if `list of stuff to do` is a single instruction, best to use curly braces
+
+```R
+if (condition is true) {
+ list of stuff to do
+} else if (another condition) {
+ ...
+} else {
+ ...
+}
+```
+
+---
+
+# `for` loops
+
+`for` applies to lists or vectors
+
+```R
+for (i in 1:10) {
+ something using integer i
+}
+for (j in c(1,3,4)) {
+ something using integer j
+}
+for (n in c("truc", "muche", "chose")) {
+ something using string n
+}
+for (m in list("truc", "muche", "chose", 1, 2)) {
+ something using string n or integer n, depending
+}
+```
+
diff --git a/SLIDES/lecture-05-flow-control.md b/SLIDES/vignette-06-apply-lapply-and-friends.md
similarity index 96%
rename from SLIDES/lecture-05-flow-control.md
rename to SLIDES/vignette-06-apply-lapply-and-friends.md
index 2597fd5..bb1ab88 100644
--- a/SLIDES/lecture-05-flow-control.md
+++ b/SLIDES/vignette-06-apply-lapply-and-friends.md
@@ -3,9 +3,10 @@ marp: true
title: R for modellers - Lecture 01 - Introduction to R. Installing R
description: Julien Arino - Lecture 01 - R for modellers - Introduction to R. Installing R.
theme: default
-paginate: false
+class: invert
math: mathjax
-size: 16:9
+paginate: false
+size: 4:3
---
+
+
+
+
+# Lecture 10 - Solving ODE
+
+Julien Arino [](mailto:Julien.Arino@umanitoba.ca) [](https://julien-arino.github.io/) [](https://github.com/julien-arino)
+
+Department of Mathematics
+University of Manitoba*
+
+
+
+Canadian Centre for Disease Modelling
+
+
+* The University of Manitoba campuses are located on original lands of Anishinaabeg, Cree, Oji-Cree, Dakota and Dene peoples, and on the homeland of the Métis Nation.
+
+---
+
+
+# Outline
+
+- The deSolve library
+
+---
+
+
+# The deSolve library
+
+---
+
+# The deSolve library
+
+- As I have already pointed out, [`deSolve`](https://cran.r-project.org/web/packages/deSolve/index.html):
+> The functions provide an interface to the FORTRAN functions 'lsoda', 'lsodar', 'lsode', 'lsodes' of the 'ODEPACK' collection, to the FORTRAN functions 'dvode', 'zvode' and 'daspk' and a C-implementation of solvers of the 'Runge-Kutta' family with fixed or variable time steps
+
+---
+
+- You are benefiting from years and years of experience: [ODEPACK](https://computing.llnl.gov/projects/odepack) is a set of Fortran (77!) solvers developed at Lawrence Livermore National Laboratory (LLNL) starting in the late 70s
+
+- Other good solvers written in `C` are also included
+
+- Refer to the [package help](https://cran.r-project.org/web/packages/deSolve/deSolve.pdf) for details
+
+---
+
+# Using deSolve for simple ODEs
+
+As with more numerical solvers, you need to write a function returning the value of the right hand side of your equation (the vector field) at a given point in phase space, then call this function from the solver
+
+```R
+library(deSolve)
+rhs_logistic <- function(t, x, p) {
+ with(as.list(x), {
+ dN <- p$r * N *(1-N/p$K)
+ return(list(dN))
+ })
+}
+params = list(r = 0.1, K = 100)
+IC = c(N = 50)
+times = seq(0, 100, 1)
+sol <- ode(IC, times, rhs_logistic, params)
+```
+
+---
+
+This also works: add `p` to arguments of `as.list` and thus use without `p$` prefix
+
+```R
+library(deSolve)
+rhs_logistic <- function(t, x, p) {
+ with(as.list(c(x, p)), {
+ dN <- r * N *(1-N/K)
+ return(list(dN))
+ })
+}
+params = list(r = 0.1, K = 100)
+IC = c(N = 50)
+times = seq(0, 100, 1)
+sol <- ode(IC, times, rhs_logistic, params)
+```
+
+In this case, beware of not having a variable and a parameter with the same name..
+
+---
+
+# Default method: `lsoda`
+
+- `lsoda` switches automatically between stiff and nonstiff methods
+
+- You can also specify other methods: "lsode", "lsodes", "lsodar", "vode", "daspk", "euler", "rk4", "ode23", "ode45", "radau", "bdf", "bdf_d", "adams", "impAdams" or "impAdams_d" ,"iteration" (the latter for discrete-time systems)
+
+```
+ode(y, times, func, parms,
+ method = "ode45")
+```
+
+- You can even implement your own integration method
+
diff --git a/SLIDES/vignette-11-solving-DDE.md b/SLIDES/vignette-11-solving-DDE.md
new file mode 100644
index 0000000..5fb4780
--- /dev/null
+++ b/SLIDES/vignette-11-solving-DDE.md
@@ -0,0 +1,168 @@
+---
+marp: true
+title: Lecture 11 - Solving DDE
+description: Julien Arino - R for modellers - Lecture 10 - Solving delay differential equations (DDE) in R
+theme: default
+class: invert
+math: mathjax
+paginate: false
+size: 4:3
+---
+
+
+
+
+
+
+# Lecture 10 - Solving ODE
+
+Julien Arino [](mailto:Julien.Arino@umanitoba.ca) [](https://julien-arino.github.io/) [](https://github.com/julien-arino)
+
+Department of Mathematics
+University of Manitoba*
+
+
+
+Canadian Centre for Disease Modelling
+
+
+* The University of Manitoba campuses are located on original lands of Anishinaabeg, Cree, Oji-Cree, Dakota and Dene peoples, and on the homeland of the Métis Nation.
+
+---
+
+
+# Outline
+
+- The deSolve library
+- Example - Fitting data
+
+---
+
+
+# The deSolve library
+
+---
+
+# The deSolve library
+
+- As I have already pointed out, [`deSolve`](https://cran.r-project.org/web/packages/deSolve/index.html):
+> The functions provide an interface to the FORTRAN functions 'lsoda', 'lsodar', 'lsode', 'lsodes' of the 'ODEPACK' collection, to the FORTRAN functions 'dvode', 'zvode' and 'daspk' and a C-implementation of solvers of the 'Runge-Kutta' family with fixed or variable time steps
+
+- So you are benefiting from years and year of experience: [ODEPACK](https://computing.llnl.gov/projects/odepack) is a set of Fortran (77!) solvers developed at Lawrence Livermore National Laboratory (LLNL) starting in the late 70s
+
+- Other good solvers are also included, those written in C
+
+- Refer to the [package help](https://cran.r-project.org/web/packages/deSolve/deSolve.pdf) for details
+
+---
+
+# Using deSolve for simple ODEs
+
+As with more numerical solvers, you need to write a function returning the value of the right hand side of your equation (the vector field) at a given point in phase space, then call this function from the solver
+
+```R
+library(deSolve)
+rhs_logistic <- function(t, x, p) {
+ with(as.list(x), {
+ dN <- p$r * N *(1-N/p$K)
+ return(list(dN))
+ })
+}
+params = list(r = 0.1, K = 100)
+IC = c(N = 50)
+times = seq(0, 100, 1)
+sol <- ode(IC, times, rhs_logistic, params)
+```
+
+---
+
+This also works: add `p` to arguments of `as.list` and thus use without `p$` prefix
+
+```R
+library(deSolve)
+rhs_logistic <- function(t, x, p) {
+ with(as.list(c(x, p)), {
+ dN <- r * N *(1-N/K)
+ return(list(dN))
+ })
+}
+params = list(r = 0.1, K = 100)
+IC = c(N = 50)
+times = seq(0, 100, 1)
+sol <- ode(IC, times, rhs_logistic, params)
+```
+
+In this case, beware of not having a variable and a parameter with the same name..
+
+---
+
+# Default method: `lsoda`
+
+- `lsoda` switches automatically between stiff and nonstiff methods
+
+- You can also specify other methods: "lsode", "lsodes", "lsodar", "vode", "daspk", "euler", "rk4", "ode23", "ode45", "radau", "bdf", "bdf_d", "adams", "impAdams" or "impAdams_d" ,"iteration" (the latter for discrete-time systems)
+
+```
+ode(y, times, func, parms,
+ method = "ode45")
+```
+
+- You can even implement your own integration method
+
+---
+
+
+# Example - Fitting data
+
+---
+
+# Example - Fitting data
+
+- Note that this is a super simplified version of what to do
+- Much more elaborate procedures exist
+ - Roda. [Bayesian inference for dynamical systems](https://doi.org/10.1016/j.idm.2019.12.007)
+ - Portet. [A primer on model selection using the Akaike Information Criterion](https://doi.org/10.1016/j.idm.2019.12.010)
+- Let us grab some epi data online and fit an SIR model to it
+- Don't expect anything funky, as I said, this is the baby version
+- Also, keep in mind that any identification procedure is subject to risks due to *identifiability issues*; see, e.g., Roda et al, [Why is it difficult to accurately predict the COVID-19 epidemic?](https://doi.org/10.1016/j.idm.2020.03.001)
+
+---
+
+# Principle
+
+- Data is a set $(t_i,y_i)$, $i=1,\ldots,N$, where $t_i\in\mathcal{I}$, some interval
+- Solution to SIR is $(t,x(t))$ for $t\in\mathcal{I}$
+- Suppose parameters of the model are $p$
+- We want to minimise the error function
+$$
+E(p) = \sum_{i=1}^N \|x(t_i)-y_i\|
+$$
+- Norm is typically Euclidean, but could be different depending on objectives
+- So given a point $p$ in (admissible) parameter space, we compute the solution to the ODE, compute $E(p)$
+- Using some minimisation algorithm, we seek a minimum of $E(p)$ by varying $p$
+
+---
+
+# What are $y_i$ and $x(t_i)$ here?
+
+- In epi data for infectious diseases, we typically have incidence, i.e., number of new cases per unit time
+- In SIR model, this is $\beta SI$ or $\beta SI/N$, so, if using mass action incidence and Euclidean norm
+$$
+E(p)=\sum_{i=1}^N(\beta S(t_i)I(t_i)-y_i)^2
+$$
+or, if using standard incidence
+$$
+E(p)=\sum_{i=1}^N
+\left(\beta \frac{S(t_i)I(t_i)}{N}-y_i\right)^2
+$$
+
+---
+
+# Implementing in practice
+
+See the code [practicum_01_fitting.R](https://raw.githubusercontent.com/julien-arino/3MC-course-epidemiological-modelling/main/CODE/practicum_01_fitting.R), which we will go over now
\ No newline at end of file
diff --git a/SLIDES/vignette-12-fitting-an-ODE.md b/SLIDES/vignette-12-fitting-an-ODE.md
new file mode 100644
index 0000000..7ea7889
--- /dev/null
+++ b/SLIDES/vignette-12-fitting-an-ODE.md
@@ -0,0 +1,100 @@
+---
+marp: true
+title: Lecture 12 - Fitting an ODE
+description: Julien Arino - R for modellers - Lecture 12 - Fitting ordinary differential equations (ODE) to data in R
+theme: default
+class: invert
+math: mathjax
+paginate: false
+size: 4:3
+---
+
+
+
+
+
+
+# Lecture 12 - Fitting an ODE
+
+Julien Arino [](mailto:Julien.Arino@umanitoba.ca) [](https://julien-arino.github.io/) [](https://github.com/julien-arino)
+
+Department of Mathematics
+University of Manitoba*
+
+
+
+Canadian Centre for Disease Modelling
+
+
+* The University of Manitoba campuses are located on original lands of Anishinaabeg, Cree, Oji-Cree, Dakota and Dene peoples, and on the homeland of the Métis Nation.
+
+---
+
+
+# Outline
+- Principle - Fitting data
+- Example 1 - Kermack McKendrick SIR epidemic model
+
+---
+
+
+# Principle - Fitting data
+
+---
+
+# Fitting data
+
+- Note that this is a super simplified version of what to do
+- Much more elaborate procedures exist
+ - Roda. [Bayesian inference for dynamical systems](https://doi.org/10.1016/j.idm.2019.12.007)
+ - Portet. [A primer on model selection using the Akaike Information Criterion](https://doi.org/10.1016/j.idm.2019.12.010)
+
+---
+
+- Let us grab some epi data online and fit an SIR model to it
+- Do not expect anything funky, as I said, this is the baby version
+- Also, keep in mind that any identification procedure is subject to risks due to *identifiability issues*; see, e.g., Roda et al, [Why is it difficult to accurately predict the COVID-19 epidemic?](https://doi.org/10.1016/j.idm.2020.03.001)
+
+---
+
+# Principle
+
+- Data is a set $(t_i,y_i)$, $i=1,\ldots,N$, where $t_i\in\mathcal{I}$, some interval
+- Solution to SIR is $(t,x(t))$ for $t\in\mathcal{I}$
+- Suppose parameters of the model are $p$
+- We want to minimise the error function
+$$
+E(p) = \sum_{i=1}^N \|x(t_i)-y_i\|
+$$
+
+---
+
+- Norm is typically Euclidean, but could be different depending on objectives
+- So given a point $p$ in (admissible) parameter space, we compute the solution to the ODE, compute $E(p)$
+- Using some minimisation algorithm, we seek a minimum of $E(p)$ by varying $p$
+
+---
+
+# What are $y_i$ and $x(t_i)$ here?
+
+- In epi data for infectious diseases, we typically have incidence, i.e., number of new cases per unit time
+- In SIR model, this is $\beta SI$ or $\beta SI/N$, so, if using mass action incidence and Euclidean norm
+$$
+E(p)=\sum_{i=1}^N(\beta S(t_i)I(t_i)-y_i)^2
+$$
+or, if using standard incidence
+$$
+E(p)=\sum_{i=1}^N
+\left(\beta \frac{S(t_i)I(t_i)}{N}-y_i\right)^2
+$$
+
+---
+
+# Implementing in practice
+
+See the code [practicum_01_fitting.R](https://raw.githubusercontent.com/julien-arino/3MC-course-epidemiological-modelling/main/CODE/practicum_01_fitting.R), which we will go over now
\ No newline at end of file
diff --git a/index.md b/index.md
index 3ca2051..912ae55 100644
--- a/index.md
+++ b/index.md
@@ -8,7 +8,9 @@ Feel free to use the material in these slides or in the folders. If you find thi
### Slides
-Please note that the slides here are inherently a work in progress. I will be updating them from time to time to reflect a better understanding of the material, new packages, etc. Also note that the order of the "lectures" is, for the most part, not really relevant and is included mostly for my convenience.
+Please note that the slides here are inherently a work in progress. I will be updating them from time to time to reflect a better understanding of the material, new packages, etc.
+Contrary to other courses I have posted, these are small snapshots meant to illustrate a technique, so slide sets and videos vary greatly in length.
+Also note that the order of the "lectures" is, for the most part, not really relevant and is included mostly for my convenience.