[Tutorial] Hyperelastic Material Definition with Automatic Differentation using casADi #703
Replies: 6 comments 1 reply
-
|
Thanks for the suggestion. I'll surely try it out at some point. |
Beta Was this translation helpful? Give feedback.
-
|
I just wanted to let you know that I recently created a little module matADi which basically handles the above code snippets in a more user-friendly way. ...beside that - I'm still impressed of the development of scikit-fem. This is such an amazing project 👍🏻 |
Beta Was this translation helpful? Give feedback.
-
|
And this is a simple script: import numpy as np
import skfem as fem
from skfem.assembly import LinearForm, BilinearForm
from skfem.helpers import grad, identity
from matadi import MaterialHyperelastic
from matadi.models import neo_hooke
mat = MaterialHyperelastic(neo_hooke, C10=0.5, bulk=2.0)
right = 0.5
tol = 1e-10
m = fem.MeshHex().refined(2)
e1 = fem.ElementHex1()
e = fem.ElementVectorH1(e1)
ib = fem.Basis(m, e, intorder=1)
def P(w):
H = grad(w["displacement"])
F = H + identity(H)
return mat.gradient([F])[0]
def A(w):
H = grad(w["displacement"])
F = H + identity(H)
return mat.hessian([F])[0]
@LinearForm(nthreads=4)
def L(v, w):
return np.einsum("ij...,ij...", P(w), grad(v))
@BilinearForm(nthreads=4)
def a(u, v, w):
return np.einsum("ijkl...,ij...,kl...", A(w), grad(u), grad(v))
u = ib.zeros()
du = ib.zeros()
uv = ib.interpolate(u)
dofs = {
'left' : ib.get_dofs(lambda x: x[0] == 0.0),
'right': ib.get_dofs(lambda x: x[0] == 1.0),
}
I = ib.complement_dofs(dofs)
f = fem.asm(L, ib, displacement=uv)
K = fem.asm(a, ib, ib, displacement=uv)
for iteration in range(8):
du_D = u.copy()
du_D[dofs["right"].nodal['u^1']] = right - du_D[dofs["right"].nodal['u^1']]
system = fem.condense(K, -f, x=du_D, I=I)
du = fem.solve(*system)
norm_du = np.linalg.norm(du)
u += du
uv = ib.interpolate(u)
f = fem.asm(L, ib, displacement=uv)
K = fem.asm(a, ib, ib, displacement=uv)
print(1 + iteration, norm_du)
if norm_du < tol:
break
savedata = {"u": u[ib.nodal_dofs].T}
m.save("result.vtk", savedata)Output: 0 3.4810410954530506
1 0.13063064781292275
2 0.009208944826176955
3 4.989804896048235e-05
4 2.3408069100383187e-09
5 3.2247002135208875e-16 |
Beta Was this translation helpful? Give feedback.
-
|
The above bultin Neo-Hookean material model can be replaced by any user-defined strain energy function in terms of the deformation gradient. Stress and Elasticity tensor are carried out by automatic differentiation at reasonable speed. # ...
from matadi import MaterialHyperelastic
from matadi.math import det, transpose, trace
def strain_energy_function(F, C10, bulk):
J = det(F)
C = transpose(F) @ F
return C10 * (J**(-2/3) * trace(C) - 3) + bulk * (J - 1)**2/2
#mat = MaterialHyperelastic(neo_hooke, C10=0.5, bulk=2.0)
mat = MaterialHyperelastic(strain_energy_function, C10=0.5, bulk=2.0)
# ... |
Beta Was this translation helpful? Give feedback.
-
|
It's great, good job! I was going to try this out, already started to write some code, but you finished first. This would be good material for the eventual #712. |
Beta Was this translation helpful? Give feedback.
-
|
Hi, inspired by the linear elastic material definition of scikit-fem I tried to implement the bilinear form of a Neo-Hookean solid without calculating the fourth-order (deformation-dependent) elasticity tensor explicitely. Instead I only used variational calculus. Some first tests gave me a 2x speed-up and a really nice code representation. I'll come up with a nice example in the next days. 😎 |
Beta Was this translation helpful? Give feedback.

-
Hi @kinnala, @gdmcbain, @bhaveshshrimali,
this is not a Question, it's a tutorial - probably in favour to #441 using JAX.
I found a nice package for automatic differentiation (AD) with easy installation, good performance and straight-forward usage: casADi (LGPL licensed). To be honest, this is the first AD-package I'm happy with. I had no luck with
autograd(slow) andjax(Windows -> install ❌). At least on Windowscasadiperforms really well! I figured out how to apply deformation gradients with trailing axes to the AD-generated functions. Performance is about four times slower compared to hardcoded stress and elasticity tensors, which is very okay - at least for me. Let's take the Neo-Hookean material formulation as an example.Neo-Hookean material formulation
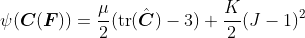
The strain energy density function (per unit undeformed volume) of the Neo-Hookean material formulation is defined as follows:
First, let's define some random deformation gradients.
I wrote a little helper class
Materialwhich provides AD-calculated functions for stress and elasticity where deformation gradient tensors with trailing axes as they are used inscikit-femare applied to the function objects generated bycasadi. If you prefer something simpler, just take theapplymethod of this class and use it as a simple function.Next, we define the strain energy density function of the Neo-Hookean material model, create an instance of the
Materialclass and calculate stress (1st Piola-Kirchhoff) and elasticity tensors.That's it! 😎
Below you'll find some checks and performance evaluations...
I compared the results with a reference implementation of the neo-hookean material used in my own package
felupe.Disclaimer: I have NOT testet this stuff yet with scikit-fem, but that shoudn't be too hard... I thought probably someone of you may find this useful!
Cheers 🏖️,
Andreas
P.S.: There is one big drawback in
casadi- if-statements...Beta Was this translation helpful? Give feedback.
All reactions