Adaptively-thresholded Low Rank Approximation (ALRA)

Introduction

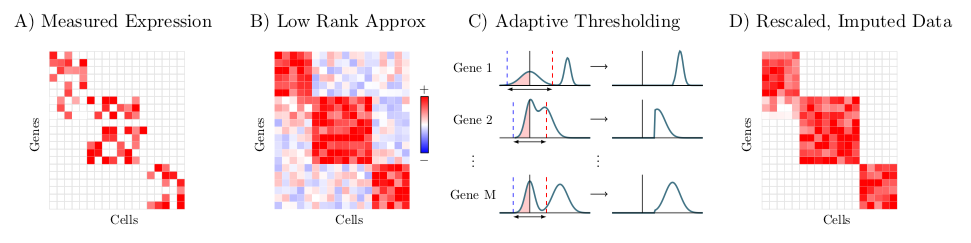
ALRA is a method for imputation of missing values in single cell RNA-sequencing data, described in the preprint, "Zero-preserving imputation of scRNA-seq data using low-rank approximation" available here. Given a scRNA-seq expression matrix, ALRA first computes its rank-k approximation using randomized SVD. Next, each row (gene) is thresholded by the magnitude of the most negative value of that gene. Finally, the matrix is rescaled.

This repository contains codes for running ALRA in R. The only prerequisite for ALRA is installation of the randomized SVD package RSVD which can be installed as install.packages('rsvd').

The functions now have a flag use.mkl for users who have installed rpca-mkl, which allows for dramatic speedups over the default rpca-based version. Note that rpca-mkl is still under development and is not on CRAN, so it is not a required package, but if users have already installed it then they can use it by setting this flag to True.

Install

ALRA can be installed as follows:

install.packages("devtools")
devtools::install_github("KlugerLab/ALRA")

Usage

Please be sure to pass ALRA a matrix where the cells are rows and genes are columns.

ALRA can be used as follows:

library(ALRA)

# Let A_norm be a normalized expression matrix where cells are rows and genes are columns.
# We use library and log normalization, but other approaches may also work well.
result.completed <- alra(A_norm)
A_norm_completed <- result.completed[[3]]

Example

library(ALRA)

data("b_nk_example")
data("labels_example")

Library and log normalize the data

A_norm <- normalize_data(b_nk_example)

Choose k.

k_choice <- choose_k(A_norm)

For the results in the paper, automatically chosen k worked quite well, but in some cases you might want to take a closer look, as we do here. The k is chosen based on the spacings between the singular values, as it can be quite hard to identify the ``beginning of noise'' from just looking at the spectrum itself.

library(ggplot2)
library(gridExtra)
df <- data.frame(x=1:100,y=k_choice$d)
g1<-ggplot(df,aes(x=x,y=y),) + geom_point(size=1)  + geom_line(size=0.5)+ geom_vline(xintercept=k_choice$k)   + theme( axis.title.x=element_blank() ) + scale_x_continuous(breaks=seq(10,100,10)) + ylab('s_i') + ggtitle('Singular values')
df <- data.frame(x=2:100,y=diff(k_choice$d))[3:99,]
g2<-ggplot(df,aes(x=x,y=y),) + geom_point(size=1)  + geom_line(size=0.5)+ geom_vline(xintercept=k_choice$k+1)   + theme(axis.title.x=element_blank() ) + scale_x_continuous(breaks=seq(10,100,10)) + ylab('s_{i} - s_{i-1}') + ggtitle('Singular value spacings')
grid.arrange(g1,g2,nrow=1)

A_norm_completed <- alra(A_norm,k=k_choice$k)[[3]]

Check the completion. Note that the results improve when using the entire dataset (see the ALRA-paper repo for those codes), as opposed to this subset.

• NCAM1 should be expressed in all NK cells, but is only expressed in 4% of of NK cells in the original data.
• CR2 should be expressed in all B cells, but is only expressed in 1% of of B cells in the original data.

print(aggregate(A_norm[,c('NCAM1','CR2')], by=list(" "=labels_example),FUN=function(x) round(c(percent=100*sum(x>0)/length(x)),1)))
print(aggregate(A_norm_completed[,c('NCAM1','CR2')], by=list(" "=labels_example),FUN=function(x) round(c(percent=100*sum(x>0)/length(x)),1)))

More info

ALRA is integrated into Seurat v3.0 (currently at pre-release stage) as function RunALRA(). But if you use Seurat v2, we provide a simple function to perform ALRA on a Seurat v2 object in alraSeurat2.R.

ALRA is supported for OS X, Linux, and Windows. It has been tested on MacOS (Mojave, 10.14) and Ubuntu 16.04. Installation should not take longer than a minute or two.